Função do segundo grau - Introdução
Uma função do segundo grau ou quadrática tem a seguinte caraterística:
Exemplos:
5) (PUC - RS 2004) Em uma fábrica, o número total de peças produzidas t horas diárias de trabalho é dado por
O número de peças produzidas durante a quinta hora de trabalho é:
a) 40 b) 200 c) 1000 d) 1200 e) 2200
Desta forma, a alternativa correta é a d.
6) ( Furb - SC 2003) O gráfico abaixo representa uma função quadrática:  . Os valores de a, b e c, respectivamente, são:
. Os valores de a, b e c, respectivamente, são:
a) -1, -2 e -1 b) 1, -2 e 1 c)-1,-2 e 1 d) -1, 2 e -1 e) 1, 2 e 1
Observando o gráfico, temos:
Para x = 2, y = -1:
Para x = 1 , y = 0 :
Para x = 0, y = -1:
Substituindo ( III ) em ( II ), temos:
Substituindo ( IV ) em ( I ), temos:
Desta forma, a alternativa correta é a d.
7) (FGV - SP 2003 ) Seja a função 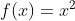 . O valor de f( m + n) - f(m - n) é:
. O valor de f( m + n) - f(m - n) é:
Temos:
Então:
Desta forma, a alternativa correta é a c.
8) ( Vunesp - SP ) O gráfico da função quadrática definida por  , onde m é um úmero real, tem um único ponto em comum com o eixo das abscissas. Então, o valor de y que essa função associa a x = 2 é:
, onde m é um úmero real, tem um único ponto em comum com o eixo das abscissas. Então, o valor de y que essa função associa a x = 2 é:
a) -2 b) -1 c) 0 d) 1 e) 2
Conforme o enunciado, a função tem um único pontoem comum com o eixo das abscissas, ou seja, o seu gráfico corta o eixo x em um único ponto. Desta forma, concluímos que 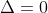 .
.
Para x = 2, temos:
Desta forma, a alternativa correta é a d.
9. ( UFPI ) Uma fábrica produz  pares de sapatos t horas após o início de suas atividades diárias. Se a fábrica começa a funcionar às 8 hs da manhã, entre 10 e 11 horas serão produzidos:
pares de sapatos t horas após o início de suas atividades diárias. Se a fábrica começa a funcionar às 8 hs da manhã, entre 10 e 11 horas serão produzidos:
a) 7 pares de sapatos b) 8 pares de sapatos c) 15 pares de sapatos d) 23 pares de sapatos
Nas três horas de produção ( das 8 às 11 hs ), teremos a seguinte produção:
Das 8 às 10 hs, teremos a seguinte produção:
Desta forma, entre 10 e 11 hs teremos a seguinte produção:
Desta forma, a alternativa correta é a a.
1. Concavidade da parábola
O gráfico de uma função quadrática é uma parábola.
Se 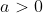 , a parábola terá a sua concavidade voltada para cima.
, a parábola terá a sua concavidade voltada para cima.
Se  , a parábola terá a sua concavidade voltada para baixo.
, a parábola terá a sua concavidade voltada para baixo.
Exemplos:
Observemos que :
Observemos que :
2. Raízes ou zeros de uma função quadrática
Os zeros ou raízes de uma função quadrática são os valores de x, tais que f(x) = 0.
Exemplos:
Determine as raízes reais de cada uma das funções abaixo:
Raízes: 1 e 2.
Raízes: -2.







- Follow Us on Twitter!
- "Join Us on Facebook!
- RSS
Contato