Relações métricas no triângulo retângulo

Observemos o triângulo retângulo ABC abaixo.

Conforme a figura ilustra, o triângulo ABC pode ser decomposto em dois triângulos retângulos: o triângulo ADB (em azul) e o triângulo ADC (em rosa).
Uitlizando conceitos de semelhança de triângulos, chegamos às seguintes relações métricas:

 

Podemos demonstrar o Teorema de Pitágoras da seguinte forma:



Exemplos:
1. Determine as medidas desconhecidas.

2.  Calcule a altura de um triângulo retângulo, cujas projeções dos catetos medem 5cm e 8cm.

  

3. Determine  as medidas desconhecidas:

Soma de ângulos internos

1. Soma de ângulos internos de um triângulo

A soma das medidas dos ângulos internos de um triângulo é igual a 180°.

Exemplos:

1.  Abaixo, temos um triângulo equilátero, calcule as medidas dos ângulos.

Aqui temos um triângulo equilátero, logo os lados e os ângulos deste triângulo são iguais:   a = b= c =x.



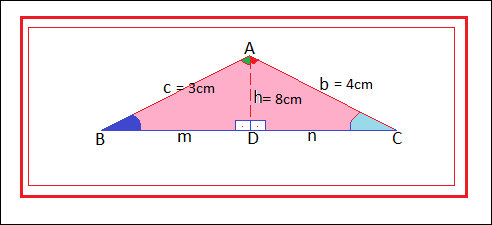
2.  Observe o triângulo isósceles e calcule a medida do ângulo da base.

Como o triângulo ABC é isósceles, os ângulos da base são iguais ( ângulo a = x e ângulo b = x).

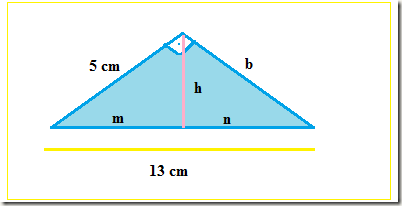
3.  Calcule as medidas desconhecidas.

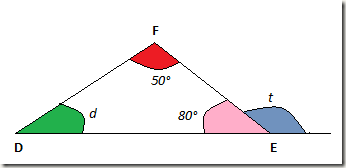
Observemos que os ângulos em rosa e em azul são suplementares, então temos:



A partir da soma dos ângulos internos do triângulo, podemos calcular o ângulo d:



4. Calcule as medidas dos ângulos do triângulo abaixo.

  

2. Soma de ângulos internos de um polígono

Para um polígono de n  lados, a soma dos ângulos internos deste é dada por:

Exemplos:

1. Calcule a soma dos ângulos internos de um pentágono.

2. Calcule a soma dos ângulos internos de um icoságono.

Um icoságono é um polígono com 20 lados.

3.  Observe a  figura abaixo e calcule x+y+z. Os polígonos são regulares.

Como os polígonos são regulares, podemos concluir que todos os lados e ângulos são iguais.

Desta forma, ao observarmos os triângulos azuis, concluímos que:

No centro do nosso polígono, temos um hexágono e a soma das medidas de seus ângulos internos é dada por:

Logo, a medida do ângulo z é:

Assim, temos: