Determinantes

1. Determinante de uma matriz de ordem 1

Dada uma matriz A quadrada de ordem 1 $\left (A=\left [ a_{11} \right ] \right )$ , o seu determinante será o termo $a_{11}$ .

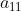Exemplos:

$A=\begin{bmatrix} -9 \end{bmatrix}$ $det A=-9$

$X=\begin{bmatrix} 0 \end{bmatrix}$ $det X=0$

2. Determinante de uma matriz de ordem 2

Dada uma matriz A quadrada de ordem 2, o seu determinante será calculado através do produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária:

$A=\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix}$ $detA=a_{11}.a_{22}-a_{12}.a_{21}$ ou $\begin{vmatrix} a_{11} &a_{12} \\ a_{21}& a_{22} \end{vmatrix}=a_{11}.a_{22}-a_{12}.a_{21}$

Exemplos:

1) Calcule os determinantes:

$a)\begin{vmatrix} -6 & 8\\ 3 & \frac{1}{2} \end{vmatrix}$ $b)A=\begin{bmatrix} 2x & 1\\ y+4 & 3x \end{bmatrix}$

$a)\begin{vmatrix} -6 &8 \\ 3 & \frac{1}{2} \end{vmatrix}=\left ( -6 \right ).\frac{1}{2}-8.3=-3-24=-27$

$b)detA=\begin{vmatrix} 2x & 1\\ y+4 & 3x \end{vmatrix}=2x.3x-1.\left ( y+4 \right )=6x^{2}-y-4$

2) Sendo $a=\begin{vmatrix} 1 & 2\\ 3 & 4 \end{vmatrix}$ e $b=\begin{vmatrix} 5 & 6\\ 7 & 8 \end{vmatrix}$ , calcule o valor de $a^{2}+b^{3}$ .

$a=\begin{vmatrix} 1 & 2\\ 3 &4 \end{vmatrix}=1.4-2.3=-2$ $b=\begin{vmatrix} 5 & 6\\ 7 &8 \end{vmatrix}=5.8-7.6=-2$

$a^{2}+b^{3}=\left ( -2 \right )^{2}+\left ( -2 \right )^{3}=-4$

3) Dadas as matrizes

$A=\begin{bmatrix} -2 & 0\\ 1 & 2 \end{bmatrix}$ e $B=\begin{bmatrix} 2 & -1\\ 1 & -2 \end{bmatrix}$ , calcule:

$a)detA$ $b)2.detB$ $c)det\left ( A-B \right )$ $d)detA.detB$ $e)det\left ( A.B \right )$ $f)det\left (A^{2} \right )$

$a) detA=\begin{vmatrix} -2 &0 \\ 1& 2 \end{vmatrix}=\left ( -2 \right ).2-0.1=-4$

$b) 2.detB=2.\begin{vmatrix} 2 &-1 \\ 1& -2 \end{vmatrix}=2.\left ( 2.\left ( -2 \right )-\left ( -1 \right ).1 \right )=2.\left ( -3 \right )=-6$

$c)det\left ( A-B \right )$

$A-B=\begin{bmatrix} -2-2 & 0-(-1)\\ 1-1& 2-(-2) \end{bmatrix}=\begin{bmatrix} -4 & 1\\ 0 & 4 \end{bmatrix}$

$det\left ( A-B \right )=\begin{vmatrix} -4 & 1\\ 0 & 4 \end{vmatrix}=\left ( -4 \right ).4-1.0=-16$

$d)detA.detB=\left ( -4 \right ).\left ( -6 \right )=24$

$e)det(A.B)$

$A.B=\begin{bmatrix} \left ( -2 \right ).2+0.1 &\left ( -2 \right ).\left ( -1 \right )+0.\left ( -2 \right ) \\ 1.2+2.1 & 1.\left ( -1 \right )+2.\left ( -2 \right ) \end{bmatrix}=\begin{bmatrix} -4 & 2\\ 4 & -5 \end{bmatrix}$

$det\left ( A.B \right )=\begin{vmatrix} -4 & 2\\ 4 & -5 \end{vmatrix}=\left ( -4 \right ).\left ( -5 \right )-2.4=12$

$f)det\left (A^{2} \right )$

$A^{2}=A.A=\begin{bmatrix} -2 &0 \\ 1 & 2 \end{bmatrix}.\begin{bmatrix} -2 & 0\\ 1& 2 \end{bmatrix}$

$A^{2}=\begin{bmatrix} \left ( -2 \right ).\left ( -2 \right )+0.1 & \left ( -2 \right ).0+0.2\\ \1.\left ( -2 \right )+2.1 & 1.0+2.2 \end{bmatrix}=\begin{bmatrix} 4 &0 \\ 0 & 4 \end{bmatrix}$

$det\left (A^{2} \right )=\begin{vmatrix} 4 &0 \\ 0& 4 \end{vmatrix}=4.4-0.0=16$

4) Vunesp - SP Considere a matriz $A=\left (a_{ij} \right )_{2x2}$ definida por $a_{ij}=-1+2i+j$ . O determinante de A é:

a) 22 b) 2 c) 4 d) -2 e) -4

$a_{11}=-1+2.1+1=2$ $a_{12}=-1+2.1+2=3$

$a_{21}=-1+2.2+1=4$ $a_{22}=-1+2.2+2=5$

$A=\begin{bmatrix} a_{11} &a_{12} \\ a_{21}& a_{22} \end{bmatrix}=\begin{bmatrix} 2 & 3\\ 4 & 5 \end{bmatrix}$

$detA=\begin{vmatrix} 2 & 3\\ 4 & 5 \end{vmatrix}=2.5-3.4=-2$

Desta forma, a alternativa correta é a d.

5) Mackenzie - SP O conjunto solução de

$\frac{\begin{vmatrix} 1 &x \\ 1 & 1 \end{vmatrix}}{\begin{vmatrix} 1 &1 \\ x & 1 \end{vmatrix}}=\begin{vmatrix} 1 & 1\\ x & 1 \end{vmatrix}$ é:

$a)\left \{ x\epsilon \mathbb{R}/x\neq 1 \right \}$ $b)\left \{ 0,1 \right \}$ $c)\left \{ 1 \right \}$ $d)\left \{ -1 \right \}$ $e)\left \{ 0 \right \}$

$\begin{vmatrix} 1 &x \\ 1 &1 \end{vmatrix}=1.1-x.1=1-x$ $\begin{vmatrix} 1 &1 \\ x &1 \end{vmatrix}=1.1-1.x=1-x$

$\frac{\begin{vmatrix} 1 & x\\ 1 &1 \end{vmatrix}}{\begin{vmatrix} 1 &1 \\ x & 1 \end{vmatrix}}=\begin{vmatrix} 1 & 1\\ x& 1 \end{vmatrix}\Rightarrow \frac{1-x}{1-x}=1-x$

$1=1-x\Rightarrow x=0$

Desta forma, a alternativa correta é a e.

6) PUC-RS Dadas as matrizes $x=\begin{bmatrix} 2 & 2 &2 \end{bmatrix}$ e $y=\begin{bmatrix} 2\\2 \\ 2 \end{bmatrix}$ , o determinante x.y vale:

a) 2 b) 4 c) 6 d)8 e)12

$x.y=\begin{bmatrix} 2 & 2 &2 \end{bmatrix}\begin{bmatrix} 2\\ 2 \\2 \end{bmatrix}=\begin{bmatrix} 2.2+2.2+2.2 \end{bmatrix}=\begin{bmatrix} 12 \end{bmatrix}$

$det (x.y)=\begin{vmatrix} 12 \end{vmatrix}=12$

Desta forma, a alternativa correta é a e.

3. Determinante de uma matriz de ordem 3 - Regra de Sarrus

Dada uma matriz qualquer de ordem 3, podemos calcular o seu determinante através da Regra de Sarrus:

$A=\begin{bmatrix} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} & a_{33} \end{bmatrix}$

Para calcularmos o determinante da matriz A , pela regra de Sarrus, repetiremos as duas primeiras colunas da matriz e faremos os produtos dos seus termos seguindo as diagonais da seguinte forma:

👆 fonte: https://pt.wikipedia.org/wiki/Regra_de_Sarrus

$det A= \left (a_{11}.a_{22}.a_{33}+a_{12}.a_{23}.a_{13}.a_{21}.a_{32} \right )-\left ( a_{31}.a_{22}.a_{13}+a_{32}.a_{23}.a_{11}+a_{33}.a_{21}.a_{12} \right )$

Exemplos:

1) Calcule, usando a Regra de Sarrus, os valores dos determinantes abaixo:

$A=\begin{bmatrix} -1 & 3&1 \\ 4& 1 & 10\\ -2 & 2 &0 \end{bmatrix}$

$det A=\begin{vmatrix} -1 & 3 &1 \\ 4 & 1 & 10\\ -2& 2 & 0 \end{vmatrix}=\begin{vmatrix} -1 &3 & 1 &-1 & 3\\ 4& 1 &10 &4 &1 \\ -2& 2 &0 &-2 & 2 \end{vmatrix}$

$det A=\left \{ \left ( \left ( -1 \right ).1.0+3.10.(-2)+1.4.2 \right )-\left ( 3.4.0+(-1).10.2+1.1.(-2) \right ) \right \}$

$det A=-52-(-22)=-30$

$D=\begin{vmatrix} 3 & \log_ { 3 }3 &-3 \\ 5 &\log_{3}81 & \log_{5}25\\ 7& \log_{2}8 & 8 \end{vmatrix}$

$\log_{3}3=1$ $\log_{3}81=\log_{3}3^{4}=4$ $\log_{5}25=\log_{5}5^{2}=2$

$\log_{2}8=\log_{2} 2^{3}=3$

Assim, termos:

$D=\begin{vmatrix} 3 & 1& -3\\ 5 &4 & 2\\ 7 &3 &8 \end{vmatrix}$ $D=\begin{vmatrix} 3 &1 & -3 & 3 &1 \\ 5 & 4 & 2 & 5 &4 \\ 7 & 3 & 8 &7 & 3 \end{vmatrix}$

$D=\left \{ \left ( 3.4.8+1.2.7+(-3).5.3 \right )-\left ( 1.5.8+3.2.3+(-3).4.7 \right ) \right \}$

$D=65-\left ( -26 \right )=91$

2) Dada a a matriz A, calcule os valores de z e w, sabendo-se que o traço de A vale 16 e detA=165.

. $A=\begin{bmatrix} 5 &0 & -1\\ 3 & z &-4 \\ -2 & w & 8 \end{bmatrix}$

* O traço de uma matriz quadrada é a soma dos elementos da diagonal principal desta. Assim temos:

$5+z+8=16\Rightarrow z=3$ e $A=\begin{bmatrix} 5 & 0& -1\\ 3 & 3 & -4\\ -2 & w & 8 \end{bmatrix}$

$det A=165\Rightarrow \begin{vmatrix} 5 & 0 & -1\\ 3 & 3 & -4\\ -2 &w & 8 \end{vmatrix}=165$

$\begin{vmatrix} 5 & 0 & -1 & 5 &0 \\ 3 & 3 &-4 &3 &3 \\ -2 & w & 8 &-2 & w \end{vmatrix}=165$

$detA=\left \{ \left ( 5.3.8+0.(-4).\left ( -2 \right )+(-1).3.w \right ) -\left ( 0.3.8+5.(-4).w+(-1).3.(-2) \right )\right \}$

$detA=\left ( -3w+120 \right )-\left ( -20w+16 \right )\Rightarrow (-3w+120)-(-20w+16)=165$

$17w+114=165\Rightarrow w=3$

3) Dadas as matrizes X e Y abaixo e det (XY)=750, calcule o valor de a.

$X=\begin{bmatrix} 1 & 1 & 0\\ 3&4 & 5\\ 0 &1 &3 \end{bmatrix} Y=\begin{bmatrix} 2 & 3 & 0\\ 8 &2 &4 \\ -1 &a & 1 \end{bmatrix}$

$X.Y=\begin{bmatrix} 1 & 1 &0 \\ 3 &4 &5 \\ 0 &1 &3 \end{bmatrix}\begin{bmatrix} 2 & 3 &0 \\ 8 &2 &4 \\ -1 &a &1 \end{bmatrix}$

$X.Y=\begin{bmatrix} 1.2+1.8+0.(-1) & 1.3+1.2+0.a &1.0+1.4+0.1 \\ 3.2+4.8+5.(-1)&3.3+4.2+5a &3.0+4.4+5.1 \\ 0.2+1.8+3.(-1)& 0.3+1.2+3a & 0.0+1.4+1.1 \end{bmatrix}$

$X.Y=\begin{bmatrix} 10 & 5 & 4\\ 33 & 17+5a & 21\\ 5 & 2+3a & 5 \end{bmatrix}$

$det\left ( XY \right )=\begin{vmatrix} 10 & 5 &4 \\ 33 &17+5a &21 \\ 5 & 2+3a &5 \end{vmatrix}=\begin{vmatrix} 10 & 5 & 4 & 10 & 5\\ 33 & 17+5a &21 & 33 &17+5a \\ 5& 2+3a & 5 & 5 &2+3a \end{vmatrix}$

$det\left ( XY \right )=\left \{10.5.(17+5a)+5.21.5+4.33.(2+3a) -\left ( 5.33.5+10.21.(2+3a)+4.(17+5a).5 \right ) \right \}$

$det\left ( XY \right )=750\Rightarrow \left ( 382a+1639 \right )-\left ( 730a+1585 \right )=750$

$a=-2$

4) UFSC-SC Considere as matrizes A e B a seguir e n = det(AB). Calcule $7^{n}$ .

$A=\begin{bmatrix} 1 &0 \\ -1 &-1 \\ 1 & 1 \end{bmatrix} B=\begin{bmatrix} 0 & 1 & 2\\ 3& 4 & 5 \end{bmatrix}$

$A.B=\begin{bmatrix} 1 &0 \\ -1 &-1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0 & 1 & 2\\ 3& 4 & 5 \end{bmatrix}=\begin{bmatrix} 1.0+0.3 & 1.1+0.4 &1.2+0.5 \\ (-1).0+(-1).3&(-1).1+(-1).4 &(-1).2+(-1).5 \\ 1.0+3.1 &1.1+1.4 & 1.2+1.5 \end{bmatrix}$

$A.B=\begin{bmatrix} 0 &1 &2 \\ -3 &-5 &-7 \\ 3 & 5 &7 \end{bmatrix}$

$n=det(AB)=\begin{vmatrix} 0 & 1 & 2 & 0 &1 \\ -3 & -5 & -7 &-3 & -5\\ 3 & 5 &7 &3 &5 \end{vmatrix}$

$n=det\left ( AB \right )=\left \{ \left ( 0.(-5).7+1.(-7).3+2.(-3).5 \right )-\left ( 1.(-3).7+0.(-7).5+2.(-5).3 \right ) \right \}$

$n=det\left ( AB \right )=-51-\left ( -51 \right )=0$

$7^{n}=7^{0}=1$

5) FGV-SP

Se $\begin{vmatrix} a & b\\ c & d \end{vmatrix}=0$ , então o valor do determinante $\begin{vmatrix} a &b &0 \\ 0 &d & 1\\ c & 0 & 2 \end{vmatrix}$ é:

$a) 0$ $b) bc$ $c) 2bc$ $d) 3bc$ $e)b ^{2}c^{2}$

$\begin{vmatrix} a & b\\ c & d \end{vmatrix}=0\Rightarrow ad-bc=0\Rightarrow ad=bc$

$\begin{vmatrix} a & b & 0\\ 0 &d &1 \\ c& 0 & 2 \end{vmatrix}=\begin{vmatrix} a & b &0 & a & b\\ 0 & d &1 & 0 & d\\ c & 0 & 2 &c &0 \end{vmatrix}=\left \{ \left ( a.d.2+b.1.c+0.0.0 \right )-\left ( b.0.2+a.1.0+0.d.c \right ) \right \}$

$\begin{vmatrix} a & b & 0\\ 0 &d &1 \\ c& 0 & 2 \end{vmatrix}=2ad+bc=2.(bc)+bc=3bc$

Desta forma, a alternativa correta é a d.

4. Determinante de uma matriz de ordem n.

Podemos calcular o determinante de uma matriz de ordem n, a partir de determinantes de matrizes de ordem n-1.

4.1. Menor complementar

Seja uma matriz A de ordem 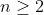$n\geq 2$ , determinaremos o menor complementar de A , escolhendo-se um elemento 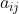$a_{ij}$ e retirando-se a linha e coluna que contém este elemento .

Exemplos:

1) Dada a matriz A, calcule $D_{21}$ , $D_{22}$ e $D_{23}$ .

$A=\begin{bmatrix} 2 & 4 & 3\\ 5 & 2 &1 \\ -3 & 7 & -1 \end{bmatrix}$

$D_{21}$ : menor complementar de A pelo elemento $a_{21}$ :

$D_{21}=\begin{vmatrix} 4 &3 \\ 7 & -1 \end{vmatrix}=4.(-1)-3.7=-25$

$D_{22}$ : menor complementar de A pelo elemento $a_{22}$ :

$D_{22}=\begin{vmatrix}2 &3 \\ -3 & -1 \end{vmatrix}=2.(-1)-3.(-3)=7$

$D_{23}$ : menor complementar de A pelo elemento $a_{23}$ :

$D_{23}=\begin{vmatrix}2 &4 \\ -3 & 7 \end{vmatrix}=2.7-4.(-3)=26$

2) Dada a matriz B, calcule o menor complementar pelo termo 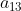$a_{13}$ .

$B=\begin{bmatrix} 1 & 5 & 9 & 13\\ 2 &6 & 10 &14 \\ 3 &7 & 11 &15 \\ 4 & 8 &12 &16 \end{bmatrix}$

Teremos que retirar a segunda linha e a terceira coluna para determinarmos o menor complementar $D_{13}$

$D_{13}=\begin{vmatrix} 2 & 6 & 14\\ 3 & 7 & 15\\ 4 & 8 &16 \end{vmatrix}=\begin{vmatrix} 2 & 6 & 14 & 2 & 6\\ 3 & 7 &15 &3 & 7\\ 4 & 8 &16 &4 &8 \end{vmatrix}$

$D_{13}=\left ( 2.7.16+6.15.4+14.3.8 \right )-\left ( 6.3.16-2.15.8+4.7.14 \right )$

$D_{13}=920-920=0$

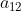3) FEI-SP Seja M uma matriz quadrada de 3ª ordem em que $a_{ij}=2i-j.$ . Então, o menor complementar do elemento $a_{12}$ vale:

a) -4 b) 7 c) 0 d) 3 e) nra

$M=\begin{bmatrix} a_{11} & a_{12} &a_{13} \\ a_{21} & a_{22} & a_{23}\\ a_{31}& a_{32} & a_{33} \end{bmatrix}$

$a_{ij}=2i-j$

$a_{11}=2.1-1=1$ $a_{12}=2.1-2=0$ $a_{13}=2.1-3=-1$

$a_{21}=2.2-1=3$ $a_{22}=2.2-2=2$ $a_{23}=2.2-3=1$

$a_{31}=2.3-1=5$ $a_{32}=2.3-2=4$ $a_{33}=2.3-3=3$

$M=\begin{bmatrix} 1 & 0 & -1\\ 3 & 2 &1 \\ 5 & 4 &3 \end{bmatrix}$

$D_{12}=\begin{vmatrix} 3 & 1\\ 5 & 3 \end{vmatrix}=3.3-1.5=4$

Desta forma, a alternativa correta é a e.

4.2. Cofator

Dada uma matriz A de ordem 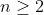$n\geq 2$ , o cofator de 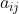$a_{ij}$ será dado por:

$A_{ij}=\left ( -1 \right )^{i+j}.D_{ij}$

$D_{ij}$ é o menor complementar de $a_{ij}$ .

Exemplos:

1) Dada a matriz A, determine o cofator do elemento 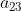$a_{23}$ .

$A=\begin{bmatrix} 1 & 1 & 3\\ 0 &2 &1 \\ -1 & 1 &2 \end{bmatrix}$

$A_{23}=\left ( -1 \right )^{2+3}.\begin{vmatrix} 1 & 1\\ -1 & 1 \end{vmatrix}=\left ( -1 \right )^{5}.\left ( 1.1-1.\left ( -1 \right ) \right )=-2$

2) Dada a matriz B,calcule o valor de $b_{21}.B_{21}$ .

$B=\begin{bmatrix} 8 & -4\\ 5 & 6 \end{bmatrix}$

$B_{21}=\left ( -1 \right )^{2+1}.D_{21}$

$D_{21}=\begin{vmatrix} -4 \end{vmatrix}=-4$

$B_{21}=\left ( -1 \right )^{2+1}.D_{21}=\left ( -1 \right )^{3}.\left ( -4 \right )=4$

$b_{21}.B_{21}=5.4=20$

3) PUC-SP O cofator do elemento 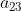$a_{23}$ da matriz A é:

$A=\begin{bmatrix} 2 & 1 &3 \\ 1 & 2 &1 \\ 0 & 1 &2 \end{bmatrix}$

a) 2 b) 1 c) -1 d) -2 e) 3

$A_{23}=\left ( -1 \right )^{2+3}.\begin{vmatrix} 2 & 1\\ 0 & 1 \end{vmatrix}=\left ( -1 \right )^{2+3}.\left ( 2.1-1.0 \right )=-2$

Desta forma, a alternativa correta é a d.

4.3. Teorema de Laplace

Podemos calcular o determinante de uma matriz quadrada de ordem 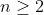$n\geq 2$ , somando-se os produtos dos elementos de uma linha (ou de uma coluna) por seus respectivos cofatores.

Exemplos:

1) Dada a matriz A,determine o seu determinante através do Teorema de Laplace.

$A=\begin{bmatrix} 2 &4 & 5\\ 3 & 0 & 2\\ 2 &8 & 1 \end{bmatrix}$

Se escolhermos os elementos da 2ª linha, teremos:

$detA=a_{21}.A_{21}+a_{22}.A_{22}+a_{23}.A_{23}$

$a_{21}.A_{21}=3.\left ( -1 \right )^{2+1}.\begin{vmatrix} 4 & 5\\ 8 & 1 \end{vmatrix}=\left ( -3 \right ).\left ( 4.1-5.8 \right )=108$

$a_{22}.A_{22}=0.A_{22}=0$

$a_{23}.A_{23}=2.\left ( -1 \right )^{2+3}.\begin{vmatrix} 2 & 4\\ 2& 8 \end{vmatrix}=\left ( -2 \right ).\left ( 2.8-4.2 \right )=-16$

$detA=108+0-16=92$

2) Aplicando o Teorema de Laplace, calcule o determinante da matriz X.

$X=\begin{bmatrix} a & 0 & 0\\ 0 & b &a \\ 0&1 &1 \end{bmatrix}$

Pelos elementos da 1ª coluna, teremos:

$detX=a_{11}.A_{11}+a_{21}.A_{21}+a_{31}.A_{31}$

$a_{11}.A_{11}=a.\left ( -1 \right )^{1+1}.\begin{vmatrix} b &a\\ 1 & 1 \end{vmatrix}=a.1.\left ( b.1-a.1 \right )=ab-a^{2}$

$a_{21}.A_{21}=0.A_{21}=0$

$a_{31}.A_{31}=0.A_{31}=0$

$detA=ab-a^{2}+0+0=ab-a^{2}$

3) FEI-SP Se

$\begin{vmatrix} 1 & 1 & 5 &1 \\ x & x^{2} &0 &1 \\ 1 & 2 & 0 & 1\\ 1 & 1 & 0 & 1 \end{vmatrix}=0$ , então:

$a) x=1$ $b) x=0$ $c) x=-2$ $d) x=-3$ $e)$ não existe x que satisfaça

Pelos elementos da 3ª coluna, teremos:

$\begin{vmatrix}1 & 1 & 5 &1 \\ x& x^{2} &0 &1 \\ 1& 2 &0 & 1\\ 1& 1 & 0 &1 \end{vmatrix}=a_{13}.A_{13}+a_{23}.A_{23}+a_{33}.A_{33}+a_{34}.A_{34}$

$a_{13}.A_{13}+a_{23}.A_{23}+a_{33}.A_{33}+a_{34}.A_{34}=0$

$a_{13}.A_{13}=5.\left ( -1 \right )^{1+3}.\begin{vmatrix} x & x^{2} &1 \\ 1 & 2 &1 \\ 1 & 1 & 1 \end{vmatrix}=5.\begin{vmatrix} x & x^{2} & 1 &x & x^{2}\\ 1 & 2 & 1 &1 &2 \\ 1 &1 & 1 & 1 &1 \end{vmatrix}$

$a_{13}.A_{13}=5.\left \{ \left ( x.2.1+x^{2}.1.1+1.1.1 \right )-\left ( x^{2}.1.1.+x.1.1+1.2.1 \right ) \right \}=5.\left ( x-1 \right )$

$a_{23}.A_{23}=0.A_{23}=0$

$a_{33}.A_{33}=0.A_{33}=0$

$a_{34}.A_{34}=0.A_{34}=0$

$\begin{vmatrix} 1 & 1 & 5 & 1\\ x & x^{2} &0 &1 \\ 1 &2 & 0 & 1\\ 1 & 1 & 0 & 1 \end{vmatrix}=0\Rightarrow a_{13}.A_{13}+a_{23}.A_{23}+a_{33}.A_{33}+a_{34}.A_{34}=0$

$5.\left ( x-1 \right )+0+0+0=0\Rightarrow x=1$

Desta forma, a alternativa correta é a a.

4) Mackenzie -SP Se

$\begin{vmatrix} 1 & 2 &1 &0 \\ 1 &1 & -2 &1 \\ 1 & -1 & 2 & -1\\ 1 &3 & 3 & x \end{vmatrix}=0$ , então o valor e x é:

$a) 0$ $b) 1$ $c) -1$ $d) -0,6$ $e) 0,6$

Pelos elementos da 4ª coluna, teremos:

$\begin{vmatrix} 1 &2 &1 &0 \\ 1 & 1 & -2 &1 \\ 1 & -1 & 2 & -1\\ 1& 3 &3 & x \end{vmatrix}=a_{14}.A_{14}+a_{24}.A_{24}+a_{34}.A_{34}+a_{44}.A_{44}$

$a_{14}.A_{14}+a_{24}.A_{24}+a_{34}.A_{34}+a_{44}.A_{44}=0$

$a_{14}.A_{14}=0.A_{14}=0$

$a_{24}.A_{24}=1.\left ( -1 \right )^{2+4}.\begin{vmatrix} 1 & 2 &1 \\ 1 & -1 & 2\\ 1 &3 &3 \end{vmatrix}=1.\begin{vmatrix} 1 & 2 & 1 &1 &2 \\ 1 & -1 & 2 & 1 & -1\\ 1 & 3 & 3 &1 &3 \end{vmatrix}$

$a_{24}.A_{24}=\left \{ \left ( 1.(-1).3+2.2.1+1.1.3 \right )-\left ( 2.1.3+1.2.3+1.(-1).1 \right ) \right \}=-7$

$a_{34}.A_{34}=\left ( -1 \right ).\left ( -1 \right )^{3+4}.\begin{vmatrix} 1 & 2 &1 \\ 1 & 1 &-2 \\ 1 & 3 & 3 \end{vmatrix}=1.\begin{vmatrix} 1 &2 &1 &1 & 2\\ 1& 1 & -2 & 1 & 1\\ 1& 3 & 3 &1 &3 \end{vmatrix}$

$a_{34}.A_{34}=\left \{ \left ( 1.1.3+2.(-2).1+1.1.3 \right )-\left ( 2.1.3+1.(-2).3+1.1.1 \right ) \right \}=1$

$a_{44}.A_{44}=x.\left ( -1 \right )^{4+4}.\begin{vmatrix} 1 & 2 & 1\\ 1 & 1 & -2\\ 1 & -1 &2 \end{vmatrix}=x.\begin{vmatrix} 1 &2 &1 & 1 &2 \\ 1 &1 &-2 &1 &1 \\ 1 &-1 &2 &1 &-1 \end{vmatrix}$

$a_{44}.A_{44}=x.\left \{ \left ( 1.1.2+2.(-2).1+1.1.(-1) \right )-\left ( 2.1.2+1.(-2).(-1)+1.1.1 \right ) \right \}$

$a_{44}.A_{44}=-10x$

$\begin{vmatrix} 1 & 2 & 1 &0 \\ 1 &1 &-2 &1 \\ 1 &-1 &2 &-1 \\ 1 & 3 &3 & x \end{vmatrix} =0\Rightarrow a_{14}.A_{14}+a_{24}.A_{24}+a_{34}.A_{34}+a_{44}.A_{44}=0$

$0+\left ( -7 \right )+1+\left ( -10x \right )=0\Rightarrow x=-0,6$

Desta forma, a alternativa correta é a d.

5. Propriedades dos determinantes

Propriedade 1: Seja A uma matriz de ordem n, o seu determinante será igual ao determinante de sua matriz transposta:

$Det A= det(A^{t})$

Exemplo:

Dada a matriz A, demonstre que a propriedade 1 $\left (Det A= det(A^{t} \right )$ é verdadeira.

$A=\begin{bmatrix} 1 &3 & 4\\ 0 & 1 &2 \\ 0 &0 &1 \end{bmatrix}$ $A^{t}=\begin{bmatrix} 1 &0 & 0\\ 3 & 1 &0\\ 4 &2 &1 \end{bmatrix}$

$detA=\begin{vmatrix} 1 & 3 & 4 &1 &3 \\ 0 & 1 & 2&0 & 1\\ 0 &0 &1 & 0 & 0 \end{vmatrix}$

$det A=\left \{ \left ( 1.1.1+3.2.0+4.0.0 \right )-\left ( 3.0.1+1.2.0+4.1.0 \right ) \right \}=1-0=1$

$det\left (A ^{t} \right )=\begin{vmatrix} 1 & 0 & 0 &1 &0 \\ 3 & 1 & 0&3 & 1\\ 4 &2 &1 & 4 & 2 \end{vmatrix}$

$det\left (A^{t} \right )=\left \{ \left ( 1.1.1+0.0.4+0.3.2 \right )-\left ( 0.3.1+1.0.2+0.1.4\right ) \right \}=1-0=1$

Conforme demonstrado acima, a propriedade 1 é verdadeira!☺

Propriedade 2: Seja A uma matriz de ordem n, na qual tenhamos uma linha ou coluna com todos os termos iguais a zero, esta terá um determinante nulo:

$detA=0$

Exemplos:

$A=\begin{bmatrix} 0 & 0\\ 1 & 2 \end{bmatrix}$ $detA=\begin{vmatrix} 0 &0 \\ 1 & 2 \end{vmatrix}=0$

$B=\begin{bmatrix} 1 & -4 & 0\\ \frac{3}{4} &-5 & 0\\ \sqrt{5}& \log_{2}4 & 0 \end{bmatrix}$ $detB=0$

Propriedade 3: Seja A uma matriz de ordem n, na qual tenhamos duas linhas iguais (ou duas colunas iguais) esta terá um determinante nulo:

$detA=0$

Exemplos:

$A=\begin{bmatrix} x &x \\ y & y \end{bmatrix}$

Observemos que a matriz A possui a 1ª coluna igual à 2ª coluna, então teremos $detA=0$ .

$X=\begin{bmatrix} 1 & \sqrt{3} & 4\\ 0 & -1 & 2\\ 1 & \sqrt{2} &4 \end{bmatrix}$

Observemos que a matriz A possui a 1ª e a 3ª linhas iguais, então teremos $detX=0$ .

Propriedade 4: Seja A uma matriz de ordem n, na qual tenhamos duas linhas proporcionais (ou duas colunas proporcionais) esta terá um determinante nulo:

$detA=0$

Exemplos:

$E=\begin{bmatrix} 1 &2 \\ 4& 8 \end{bmatrix}$ $detE=0$

Na matriz E, a 2ª linha é o quádruplo da 1ª linha, logo $detE=0$ .

$F=\begin{bmatrix} 1 & 3 & 2\\ 1 & 4 &2 \\ 1& 5 &2 \end{bmatrix} detF=0$

Na matriz F, a 3ª coluna é o dobro da 1ª coluna, logo $detF=0$ .

Propriedade 5: Dada uma matriz A de ordem n, se os elementos de uma linha (ou de uma coluna) desta forem multiplicados por uma mesmo número k, o determinante da matriz obtida será multiplicado por este número k:

$detB=k.detA$

Exemplos:

1) Dadas as matrizes A e B, calcule detB.

$A=\begin{bmatrix} a &b & c\\ d&e &f \\ g &h &i \end{bmatrix} B=\begin{bmatrix} 2a & 2b & 2c\\ d & e &f \\ g &h & i \end{bmatrix}$

Observemos que na matriz B temos a 1ª linha de A multiplicada por 2 (k=2) e as suas demais linhas (2ª e 3ª) são iguais às da matriz A. Então teremos:

$det B = 2.detA=2.10=20$

2) Dadas as matrizes A e B, calcule detB.

$A=\begin{bmatrix} a & b & c\\ d &e &f \\ g & h & i \end{bmatrix} B=\begin{bmatrix} 3a&3b & 3c\\ 3d & 3e &3f \\ 3g& 3h & 3i \end{bmatrix}$

Observemos que na matriz B temos todas as linhas de A multiplicadas por 3.Então teremos:

$detB=3.3.3.detA=27.10=270$

3) Das as matrizes A e B abaixo, calcule o determinante de B, a partir do determinante de A.

$A=\begin{bmatrix} 5 & 2& 1\\ 8 & 4 &0 \\ 7 &6 & -1 \end{bmatrix} B=\begin{bmatrix} 5 & 6 & 1\\ 8& 12 &0 \\ 7& 18 & -1 \end{bmatrix}$

Observemos que a 2ª coluna da matriz B é o triplo da 2ª coluna da matriz A, ou seja, 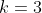$k=3$ .

Desta forma, $detB=3.detA$ .

$detA=\begin{vmatrix} 5 & 2 & 1\\ 8 & 4 & 0\\ 7 &6 &-1 \end{vmatrix}=\begin{vmatrix} 5 &2 &1 &5 &2 \\ 8 & 4 & 0 &8 &4 \\ 7 & 6 & -1 &7 &6 \end{vmatrix}$

$detA=\left \{ \left ( 5.4.(-1)+2.0.7+1.8.6 \right )-\left ( 2.8.(-1)+5.0.6+1.4.7 \right ) \right \}$

$detA=28-12=16$

$detB=3detA=3.16=48$

Propriedade 6: Dada uma matriz A de ordem n for multiplicada por um número real k,o determinante desta matriz obtida será obtido multiplicando-se o determinante da matriz A por $k^{n}$ :

$det\left ( k.A \right )=k^{n}.detA$

Exemplos:

1) Dada a matriz A, calcule $det\left ( 3A \right )$ .

$A=\begin{bmatrix} 0 & 6\\ -1 & 3 \end{bmatrix}$

$detA=\begin{vmatrix} 0 & 6\\ -1 & 3 \end{vmatrix}=0.3-6.(-1)=6$

Devemos calcular det(3A), logo temos 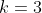$k=3$ . e n=2, pois a matriz A possui a ordem 2.

$det\left ( k.A \right )=k^{n}.detA$

$det\left ( 3A \right )=3^{2}.detA\Rightarrow det\left ( 3A \right )=9.6=54$

2) Cesgranrio - RJ Se A é matriz 3x3 de determinante 5, então det (A+A) vale:

a) 10 b) 20 c) 30 d) 40 e) 50

A matriz A é 3x3, então n=3.

det(A+A)=det(2A)⇒ k=2.

$det\left ( kA \right )=k^{n}.detA$

$det\left ( A+A \right )=2^{3}.detA\Rightarrow det(A+A)=2^{3}.5=40$

Desta forma, a alternativa correta é a d.

3) PUC - MG M é uma matriz quadrada de ordem 3, e seu determinante é det(M)=2. O valor da expressão det(M)+det(2M)+det(3M) é

a) 12 b)15 c) 36 d) 54 e) 72

M é uma matriz de ordem 3⇒ n=3.

$det\left ( kM \right )=k^{n}.detM$

$det\left ( 2M \right )=2^{3}.detM\Rightarrow det(2M)=8.2=16$

$det\left ( 3M \right )=3^{3}.detM\Rightarrow det(3M)=27.2=54$

$det\left ( M \right )+det\left ( 2M \right )+det\left ( 3M \right )=2+16+54=72$

Desta forma, a alternativa correta é a e.

4) Mackenzie - SP A e B são matrizes quadradas de ordem 3 e $B=k.A,k\epsilon \mathbb{R}$ . Sabe-se que $detA=1,5$ e $detB^{t}=96$ . Então:

a) k = 64 b) k = 96 c) k = 1/4 d) k = 3/2 e) k = 4

As matrizes e B são de ordem 3, então n=3.

$B=kA \Rightarrow det(B^{t})=det(kA)=96$

$det(kA)=k^{n}.detA$

$96=k^{3}.1,5\Rightarrow k^{3}=64\Rightarrow k=\sqrt[3]{2^{6}}=2^{2}=4$

Desta forma, a alternativa correta é a e.

Propriedade 7: Dada uma matriz A, se trocarmos de posição duas linhas (ou colunas) de posição, a matriz obtida terá como determinante o oposto do determinante da matriz A:

$detB=-detA$

Exemplo:

1) Dadas as matrizes A e B; e o determinante é 10. Calcule o determinante de B.

$A=\begin{bmatrix} a &b &c \\ d & e &f \\ g &h &i \end{bmatrix} B=\begin{bmatrix} g & h & i\\ d&e & f\\ a & b & c \end{bmatrix}$

Observemos que na matriz B há uma troca de posição entre a 1ª e a 3ª linha, logo teremos:

$detB=-detA=-10$

$A=\begin{bmatrix} 2 & 5\\ 7 & 9 \end{bmatrix} detA=\begin{vmatrix} 2 & 5\\ 7 & 9 \end{vmatrix}=-17$ $B=\begin{bmatrix} 7 & 9\\ 2 & 5 \end{bmatrix} detB=\begin{vmatrix} 7 & 9\\ 2 & 5 \end{vmatrix}=17$

Observemos que no exemplo cima, trocamos a posição das linhas e percebemos que $detB=-detA$ .

Propriedade 8: Se a matriz for triangular, o seu determinante será produto dos elementos da diagonal principal.

* Matriz triangular: todos os seus elementos abaixo ou acima da diagonal principal são nulos.

Exemplos:

$A=\begin{bmatrix} 9 & -\sqrt{2}\\ 0& 1 \end{bmatrix}$

A é uma matriz triangular, então pela propriedade temos:

$detA=9.1=9$

$B=\begin{bmatrix} 1 & 0 & 0\\ -3 &2 &0 \\ \sqrt{3} &\log_{5}125 & 3 \end{bmatrix}$

B é uma matriz triangular, então pela propriedade temos:

$detB=1.2.3=6$

Propriedade 9 - Teorema de Binet : Dadas duas matrizes quadradas de mesma ordem A e B, então teremos:

$det\left ( AB \right )=\left (det A \right ).\left ( detB \right )$

Exemplos:

1) Dadas as matrizes A e B, calcule det(AB).

$A=\begin{bmatrix} 2 &5 \\ 1& 3 \end{bmatrix} B=\begin{bmatrix} -1 & \sqrt{3}\\ 0 & 1 \end{bmatrix}$

Aplicando o Teorema de Binet, temos:

$det\left ( AB \right )=det(A).det(B)$

$det\left ( A \right )=2.3-5.1=1$

A matriz B é triangular, então temos:

$det(B)=(-1).1=-1$

Assim, temos:

$det(AB)=det(A).det(B)\Rightarrow det(AB)=1.(-1)=-1$

*Poderíamos realizar o produto das matrizes e depois calcular o seu determinante (mas pelo Teorema de Binet é muito mais simples!):

$A.B=\begin{bmatrix} 2 & 5\\ 1 & 3 \end{bmatrix}\begin{bmatrix} -1 & \sqrt{3}\\ 0& 1 \end{bmatrix}=\begin{bmatrix} 2.(-1)+5.0 & 2.\sqrt{3}+5.1\\ 1.(-1)+3.0 & 1.\sqrt{3}+3.1 \end{bmatrix}$

$A.B=\begin{bmatrix} -2 & 2\sqrt{3}+5\\ -1 & \sqrt{3}+3 \end{bmatrix}$

$det(AB)=\begin{vmatrix} -2 & 2\sqrt{3}+5\\ -1 & \sqrt{3}+3 \end{vmatrix}=\left \{ \left ( -2 \right ).\left ( \sqrt{3}+3 \right )-\left ( \left ( -1 \right ).\left ( 2\sqrt{3}+5 \right ) \right ) \right \}$

$det(AB)=-1$

2) Fuvest -SP Dadas as matrizes

$A=\begin{pmatrix} 1 & 3\\ 2& 4 \end{pmatrix} B=\begin{pmatrix} -1 & 2\\ 3& 1 \end{pmatrix}$ , o determinante da matriz A.B é:

a) -1 b) 6 c) 10 d)12 e)14

$detA=\begin{vmatrix} 1 &3 \\ 2 &4 \end{vmatrix}=1.4-3.2=-2$ $detB=\begin{vmatrix} -1 &2 \\ 3 &1 \end{vmatrix}=(-1).1-\left (2.3 \right )=-7$

$det(AB)=detA.detB\Rightarrow det(AB)=\left ( -2 \right ).\left ( -7 \right )=14$

Propriedade 10 - Teorema de Jacobi : Dada uma matriz A, se multiplicarmos todos os elemento de uma linha (ou coluna) por um mesmo número e somarmos os resultados aos elementos correspondentes de outra linha (ou coluna), obteremos uma nova matriz que terá o mesmo determinante que a matriz A:

$detB=detA$

Exemplo:

$A=\begin{bmatrix} 1 & -3 & 5\\ -1&2 & 7\\ 3 & 0 & 1 \end{bmatrix}$

Multiplicaremos a 1ª coluna da matriz A por 3 e somaremos à 3ª coluna para obtermos a matriz B:

$B=\begin{bmatrix} 1 & -3 & 8\\ -1 &2 & 4\\ 3 &0 &10 \end{bmatrix}$

Aplicando o Teorema de Jacobi teremos:

$detB=detA$

$detB=detA=\begin{vmatrix} 1 & -3 & 5\\ -1 &2 &7 \\ 3 &0 &1 \end{vmatrix}=-94$

Para verificarmos, calcularemos detB:

$detB=\begin{vmatrix} 1 & -3 & 8\\ -1 & 2 & 4\\ 3 & 0 & 10 \end{vmatrix}=\begin{vmatrix} 1 & -3 & 8 &1 & -3\\ -1& 2 & 4 &-1 &2 \\ 3& 0 & 10 &3 & 0 \end{vmatrix}$

$detB=\left \{ \left ( 1.2.10+(-3).4.3+8.(-1).0 \right )-\left ( \left ( -3 \right ).\left ( -1 \right ).10+1.4.0+8.2.3 \right ) \right \}$

$detB=-16-78=-94$

6. Regra de Chió

Como aplicação do Teorema de Jacobi é possível calcularmos determinantes a a partir de um método no qual reduziremos em uma unidade a ordem de um determinante de ordem 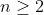$n\geq 2$ , facilitando o seu cálculo. Essa regra de abaixamento de ordem de um determinante é denominada Regra de Chió.

A Regra de Chió nos permite, a partir de um elemento igual a 1, chegarmos a um determinante de ordem menor.

Para aplicarmos a Regra de Chió, precisamos de uma matriz quadrada de ordem 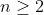$n\geq 2$ , com $a_{ij}=1.$

Há algumas etapas básicas que facilitarão a aplicação da Regra de Chió:

* eliminaremos da matriz original a linha i e a coluna j do elemento $a_{ij}=1.$

* subtrairemos de cada um dos elementos restantes da matriz A o produto dos elementos eliminados, os quais estejam na sua linha e sua coluna, obtendo assim uma nova matriz de ordem 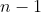$n-1$ .

* o determinante da matriz original será igual a $\left ( -1 \right )^{i+j}.detB$

Exemplos:

1) Dada a matriz A, calcule o seu determinante.

$A=\begin{bmatrix} 2 & 1 & 3 & 1\\ -1 & 2 & 5 & 1\\ 4& 1 & 3 &4 \\ 0 &0 & -2 &-1 \end{bmatrix}$

Temos $a_{12}=1$ , então eliminaremos a 1ª linha e a 2ª coluna.

Agora subtrairemos de cada um dos elementos restantes da matriz A o produto dos elementos eliminados, que estejam em sua linha e coluna:

$B=\begin{bmatrix} -1-\left ( 2.2 \right ) &5-\left ( 3.2 \right ) &1-\left ( 1.2 \right ) \\ 4-\left ( 2.1 \right )& 3-\left ( 3.1 \right ) & 4-\left ( 1.1 \right )\\ 0-\left (2.0 \right )&-2-\left ( 3.0 \right ) & -1-\left ( 1.0 \right ) \end{bmatrix}=\begin{bmatrix} -5 & -1 & -1\\ 2&0 & 3\\ 0& -2 & -1 \end{bmatrix}$

$detB=\begin{vmatrix} -5 & -1 & -1\\ 2 & 0 & 3\\ 0 & -2 & -1 \end{vmatrix}=\begin{vmatrix} -5 & -1 & -1 & -5 &-1 \\ 2 & 0 & 3 & 2 & 0\\ 0& -2 &-1 &0 & -2 \end{vmatrix}$

$detB=\left \{ \left ( \left ( -5 \right ).0.(-1)+(-1).3.0+\left ( -1 \right ).2.(-2) \right )-\left ( (-1).2.(-1)+\left ( -5 \right ).3.(-2)+(-1).0.0 \right ) \right \}$

$detB=4-32=-28$

Como escolhemos o termo 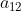$a_{12}$ , teremos:

$detA=\left ( -1 \right )^{1+2}.detB\Rightarrow detA=\left ( -1 \right ).\left ( -28 \right )=28$

2) Calcule:

$\begin{vmatrix} 1 & 2& 0 & 0\\ 2 &3 &0 & 0\\ 0 &0 & 3 & 1\\ 0 &0 &1 & 1 \end{vmatrix}$

Temos $a_{11}=1$ , então eliminaremos a 1ª linha e a 1ª coluna.

Agora subtrairemos de cada um dos elementos restantes da matriz original o produto dos elementos eliminados, que estejam em sua linha e coluna:

$B=\begin{bmatrix} 3-\left ( 2.2 \right ) & 0-\left ( 0.2 \right ) & 0-\left ( 0.2 \right )\\ 0-\left ( 2.0 \right ) & 3-\left ( 0.0 \right ) & 1-\left ( 0.0 \right )\\ 0-\left ( 2.0 \right ) &1-\left ( 0.0 \right ) & 1-\left ( 0.0 \right ) \end{bmatrix}=\begin{bmatrix} -1 & 0 &0 \\ 0&3 & 1\\ 0 &1 &1 \end{bmatrix}$

$detB=\begin{vmatrix} -1 &0 &0 \\ 0 &3 &1 \\ 0 & 1 &1 \end{vmatrix}=\begin{vmatrix} -1 & 0 &0 & -1 & 0\\ 0 & 3 & 1 & 0 & 3\\ 0 & 1 & 1 & 0 &1 \end{vmatrix}$

$detB=\left \{ \left ( (-1).3.1+0.1.0+0.0.1 \right )-\left ( 0.0.1+(-1).1.1+0.3.0 \right ) \right \}$

$detB=-3-(-1)=-2$

$\begin{vmatrix} 1 & 2 & 0 &0 \\ 2 & 3 & 0 &0 \\ 0 & 0 & 3 &1 \\ 0 & 0 & 1 & 1 \end{vmatrix}=\left ( -1 \right )^{1+1}.detB=\left ( -1 \right )^{2}.\left ( -2 \right )=-2$

3) Mackenzie -SP ~ Se o determinante mostrado na figura é igual a zero, então 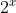$2^{x}$ pode ser:

$\begin{vmatrix} 1 & 1 & 1 &1 \\ 1 &2+2^{x} &1 &1 \\ 1 & 1 & 3-2^{x} &1 \\ 1 & 1 & 1 & 1-2^{x} \end{vmatrix}$

a) 1/2 b) 1/4 c) 1 d) 4 e) 2

Temos $a_{11}=1$ , então eliminaremos a 1ª linha e a 1ª coluna.

Agora subtrairemos de cada um dos elementos restantes da matriz original o produto dos elementos eliminados, que estejam em sua linha e coluna:

$B=\begin{bmatrix} \left ( 2+2^{x} \right )-\left (1.1 \right ) &1-\left ( 1.1 \right ) & 1-\left ( 1.1 \right )\\ 1-\left ( 1.1 \right )& \left ( 3-2^{x} \right )-\left ( 1.1 \right ) &1-\left ( 1.1 \right ) \\ 1-\left ( 1.1 \right )&1-\left ( 1.1 \right ) &\left ( 1-2^{x}-\left ( 1.1 \right ) \right ) \end{bmatrix}=\begin{bmatrix} 1+2^{x} & 0 &0 \\ 0& 2-2^{x} &0 \\ 0 &0 & -2^{x} \end{bmatrix}$

Observemos que a matriz B é triangular, então teremos:

$detB=\left ( 1+2^{x} \right ).\left ( 2-2^{x} \right ).\left ( -2^{x} \right )$

$\begin{vmatrix} 1 & 1 & 1 &1 \\ 1 &2+2^{x} &1 &1 \\ 1 &1 & 3-2^{x} &1 \\ 1 &1 & 1 & 1-2^{x} \end{vmatrix}=\left ( -1 \right )^{1+1}.detB$

$\begin{vmatrix} 1 & 1 & 1 &1 \\ 1 &2+2^{x} &1 &1 \\ 1 &1 & 3-2^{x} &1 \\ 1 &1 & 1 & 1-2^{x} \end{vmatrix}=1.\left ( 1+2^{x} \right )\left ( 2-2^{x} \right )\left ( -2^{x} \right )=\left ( 1+2^{x} \right )\left ( 2-2^{x} \right )\left ( -2^{x} \right )$

$\begin{vmatrix} 1 & 1 & 1 &1 \\ 1 &2+2^{x} &1 &1 \\ 1 &1 & 3-2^{x} &1 \\ 1 &1 & 1 & 1-2^{x} \end{vmatrix}=0\Rightarrow \left ( 1+2^{x} \right )\left ( 2-2^{x} \right )\left ( -2^{x} \right )=0$

Desta foma, teremos:

$1+2^{x}=0$ ou $2-2^{x}=0$ ou $-2^{x}=0$

$1+2^{x}=0\Rightarrow 2^{x}=-1$ Neste caso, não há solução real para x.

$-2^{x}=0$ Neste caso,também não há solução real para x.

$2-2^{x}=0\Rightarrow -2^{x}=-2\Rightarrow 2^{x}=2$

Desta forma, a alternativa correta é a e.

7. Determinante de Vandermonde

Um determinante de Vandermonde ou determiante das potências é um determinante cuja 1ª linha só possui como elementos o número 1, na 2ª linha possui quaisquer números, na 3ª os quadrados dos elementos da 2ª llinha, na 4ª os seus cubos e assim sucessivamente.

7.1. Determinante de Vandermonde de ordem 3

$\begin{vmatrix} 1 & 1 & 1\\ x & y & z\\ x^{2} &y^{2} & z^{2} \end{vmatrix}=\left ( y-x \right )\left ( z-x \right )\left ( z-y \right )$

Exemplos:

1) Dada a matriz A, calcule o seu determinante.

$A=\begin{bmatrix} 1 & 1 & 1\\ 4 & 8 & 10\\ 16 & 64 & 100 \end{bmatrix} detA=\left ( 8-4 \right )\left ( 10-4 \right )\left ( 10-8 \right )=32$

2) Calcule:

$\begin{vmatrix} 1 & 1 & 1\\ x & y & x^{3}\\ x^{2} & y^{2} & x^{6} \end{vmatrix}$

$\begin{vmatrix} 1 & 1 & 1\\ x & y & x^{3}\\ x^{2} & y^{2} & x^{6} \end{vmatrix}=\left ( y-x \right )\left ( x^{3}-x \right )\left ( x^{3}-y \right )=x^{6}y-x^{3}y^{2}+x.y^{2}-x^{7}+x^{5}-x^{2}y$

7.2. Determinante de Vandermonde de ordem 4

$\begin{vmatrix} 1 & 1 &1 &1 \\ x & y & z & w\\ x^{2} &y^{2} &z^{2} &w^{2} \\ x^{3}&y^{3} &z^{3} & w^{3} \end{vmatrix}=\left ( y-x \right )\left ( z-y \right )\left ( z-x \right )\left ( w-x \right )\left ( w-y \right )\left ( w-z \right )$

Chamaremos os elementos da 2ª linha de elementos característicos.

Um determinante de Vandermonde é calculado pelo produto de todas as diferenças obtidas pela subtração de cada um dos elementos característicos dos seus elementos precedentes.

Exemplos:

1) Dado o determinante abaixo, calcule o valor de a.

$\begin{vmatrix} 1 & 1 &1 &1 \\ a & 1 &2 &3 \\ a^{2} &1 &4 &9 \\ a^{3} &1 & 8 &27 \end{vmatrix}=0$

$\begin{vmatrix} 1 & 1 &1 &1 \\ a & 1 &2 &3 \\ a^{2} &1 &4 &9 \\ a^{3} &1 & 8 &27 \end{vmatrix}=\left ( 1-a \right )\left ( 2-a \right )\left ( 2-1 \right )\left ( 3-a \right )\left ( 3-1 \right )\left ( 3-2 \right )$

$\left ( 1-a \right )\left ( 2-a \right )\left ( 2-1 \right )\left ( 3-a \right )\left ( 3-1 \right )\left ( 3-2 \right )=0$

$1-a=0\Rightarrow a=1$ ou $2-a=0\Rightarrow a=2$ ou $3-a=0\Rightarrow a=3$

2) Calcule o determinante abaixo:

$A=\begin{vmatrix} 1 &1 & 1 & 1\\ log_{}5& log_{}50 & log_{}500 &log_{}5000 \\ \left (log_{}5 \right )^{2} & \left ( \log_{}50 \right )^{2} &\left ( \log_{}500 \right )^{2} & \left ( \log_{}5000 \right )^{2}\\ \left ( \log_{}5 \right )^{3} & \left ( \log_{} 50\right )^{3} & \left ( \log_{}500 \right )^{3} &\left ( \log_{}5000 \right )^{3} \end{vmatrix}$

$A=\left ( \log_{}50-\log_{}5 \right )\left ( \log_{}500-\log_{}50 \right )\left ( \log_{}500-\log_{}5 \right )\left ( \log_{}5000-\log_{}500 \right )\left ( \log_{}5000-\log_{}50 \right )\left ( \log_{} 5000-\log_{}5\right )$

$A=\left ( \log_{}\frac{50}{5} \right )\left ( \log_{}\frac{500}{50} \right )\left ( \log_{}\frac{500}{5} \right )\left ( \log_{}\frac{5000}{500} \right )\left ( \log{}\frac{5000}{50} \right )\left ( \log_{} \frac{5000}{5}\right )$

$A=\left (\log_{}10 \right ).\left (\log_{}10 \right ).\left (\log_{}100 \right ).\left (\log_{}10 \right ).\left (\log_{}100 \right ).\left (\log_{}1000 \right )$