Radiciação - Parte I

Radiciação

1. Raiz n-ésima de um número real

A operação de radiciação envolve o cálculo de uma raiz n-ésima de um número ().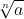

Observemos que em 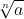, temos:  n - índice da raiz e a - radicando.

Para efetuarmos a operação de radiciação, utilizaremos o seguinte raciocínio:

Em , temos:  n - índice, a - radicando e b - raiz.

Em , temos:  n - expoente,  b - base e a - potência.

Ou seja, dados um número real 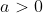  e um número natural n,teremos um número real b  tal que .

 Ao número b  chamaremos raiz n-ésima  de a :   .

Para realizarmos a operação de radiciação, faremos a decomposição do radicando (a) em fatores primos,conforme veremos explicitado em exemplos. Vale lembrar que a raiz de um número quadrado perfeito sempre é um número racional.

Potências com expoente racional

Exemplos:

1)

   e    

2)

Exemplos:

1)

, pois temos  .

 

   e   

2)

, pois temos .

3)

  

   

4)

5)

1.1.Raiz quadrada de um número real

Sendo a  um número real, para calcularmos a raiz quadrada de a, buscaremos o número que, multiplicado por si mesmo, resultará em a.

Exemplos:

1)

* Neste caso, percebemos que 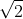 é um número irracional.

2)

*Neste caso, temos uma raiz  exata, pois a raiz quadrada é um número racional.

3)

Observemos que 729 é um número quadrado perfeito, logo terá uma raiz exata!

4)

   e   

5)

     e     

6)

    e   

7)

     e   .

1.2.Raiz n-ésima  de um número real

1.2.1 Raiz n-ésima com índice par

Os números positivos possuem duas raízes  de índice par,uma positiva e uma negativa:

  ( n par )  e  ( a > 0 ), teremos duas soluções:    e    .

*Obs: Não existe, no campo dos números reais, raiz de índice par de um número negativo.

Exemplos:

1)

     e    .

2)

      e  

3)

Esta raiz não existe no campo dos números reais, pois não existe raiz co índice par ( no caso n=6) de um número negativo!

1.2.2. Raiz n-ésima com índice ímpar

Dados um número real 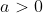 e um número natural n,teremos um número real  b  tal que .

Exemplos:

1)

2)

3)

2. Propriedades da Radiciação

2.1. Produto de radicais de mesmo índice

Exemplos:

1)

2)

3)

4)

2.2. Divisão de radicais de mesmo índice

      

Exemplos:

1)

2)

3)

2.3. Potência  de uma raiz

Exemplos:

1)

2)

2.4. Raiz de outra raiz

Exemplos:

1)

2)

2.5.Simplificação de radicais

     

Exemplos:

1)

* Observemos que  , ou seja ,    e 

.

2)

*Observemos que , ou seja,   e  

.

Também é possível dividirmos o índice do radical e o índice do radicando por um fator comum:

Exemplos:

1)

Observemos que   e  .

2)

Observemos que   e  .

3. Simplificação de Radicais

Quando realizamos a simplificação de radicais, estamos buscando uma forma mais simples de escrever estes radicais.

Exemplos:

1)

2)

4. Redução de radicais ao mesmo índice

Na operação de redução de radicais ao mesmo índice, calcularemos o índice comum de todos os radicais através do cálculo do m.m.c. dos radicais, dividiremos o índice obtido por todos os índices iniciais e multiplicaremos o resultado pelos expoentes dos fatores de cada radicando.

Exemplos:

1)

,   e  

m.m.c.(2,5,6) = 30

2)

,    e   

m.m.c.(2,4,7) = 28

5. Operações algébricas envolvendo radicais

5.1. Adição algébrica com radicais

Exemplos:

1)

Sendo assim, temos:

2)

Sendo assim, temos:

3)

Sendo assim, temos:

4)

Sendo assim, temos:

5) Determine o perímetro do retângulo abaixo:

 Use  

Perímetro  =  

6) Determine o valor de  x+3y, sendo :

      e      .

Sendo assim,temos:

7) Dados  e  , calcule o valor de .

Sendo assim, temos:

8) Fuvest - SP

 é igual a :

                            

Sendo assim,a alternativa correta é a  d.

8) Unimep - SP - 2004

O numeral mais simples que podemos dar à expressão  é:

a) 0      b) 5/2    c) 2/3     d)16/3    e) nenhuma das alternativas anteriores

 

Sendo assim, temos:

Sendo assim,a alternativa correta é a  b.

5.2. Multiplicação e divisão com radicais

Exemplos:

1)

2)

3)

As duas raízes possuem índices diferentes, então teremos que reduzí-las a um denominador comum:

m.m.c ( 2,3 ) = 6

          

4)

As duas raízes possuem índices diferentes, então teremos que reduzí-las a um denominador comum:

m.m.c ( 3,4 ) = 12

5) UPF-RS 2002 Sendo  , então 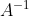  vale:

a)  4         b) 8      c) 1/4        d) 1/8          e) 14

Desta forma, a alternativa correta é a  e.

6) Inatel - MG 2003

O quociente de     por    é:

                  

Sendo assim:

Desta forma, a alternativa correta é a  c.

5.3.Potenciação e radiciação com radicais

A potenciação com radicais é realizada da seguinte forma:

Exemplos:

1)

2)

❤No próximo post sobre radiciação, exploraremos a racionalização de denominadores, então aprenderemos a retirar as raízes dos denominadores.

3)

4)

A radiciação com radicias é realizada da seguinte forma:

Exemplos:

1)

2)

3)

❤ Teremos um próximo post envolvendo o tema de Radiciação. Até breve!