Formas da equação da reta
Equação geral da reta
Qualquer reta pode ser escrita de uma forma geral:
Há algumas situações específicas:
(A) 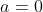 e
e 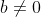 - reta paralela ao eixo x.
- reta paralela ao eixo x.
(B) 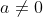 e
e 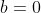 - reta paralela ao eixo y.
- reta paralela ao eixo y.
(C) 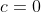 - reta passa pela origem.
- reta passa pela origem.
A equação geral da reta pode ser obtida pelo método da equação fundamental (I) ou a partir do determinante das coordenadas dos pontos da reta (II).
(I) 
(II)
Exemplos:
1) Determine a equação geral das retas abaixo:
a)
Observemos que a reta r passa pelos pontos (-2,0) e (0,4). Assim, temos:
Equação geral da reta: 
b)
Observemos que a reta r passa pelos pontos (-1/3,0) e (0,-3). Assim, temos:
Escolhemos o ponto (0,-3) e obteremos a equação geral da reta s:
Equação geral da reta s: 
c)
A reta t passa pelos pontos (0,-2) e (3,0).
Agora utilizaremos o método do determinante para encontrarmos a equação geral da reta t:
Equação geral da reta t:
2) Determinar a equação da reta r que passa pelo centro do círculo e pelo ponto A(3,3).
Observemos que a reta r passa pelos pontos A(3,3) e pelo centro do círculo(4,5).
Agora determinaremos a equação geral da reta r:
Equação da reta r: 
3) ( Fuvest - SP ) Duas retas s e t do plano cartesiano se interceptam no ponto (2,2). O produto de seus coeficientes angulares é 1 e a reta s intercepta o eixo dos y no ponto (0,3). A área do triângulo delimitado pelo eixo dos x e pelas retas s e t é:
a) 2 b) 3 c) 4 d) 5 e) 6
A reta s passa pelos pontos (2,2) e (0,3):
Equação da reta t:
Consideremos um ponto qualquer da reta t, se y = 0 , temos:
Ponto (3,0).
Agora vamos visualizar as retas nos eixos:
A área do triângulo é dada por:
Desta forma,a alternativa correta é a b.
4) (UFSCar - SP) No plano cartesiano, seja r uma reta de equação ax + 2y - 2 = 0. Sabendo que
P = ( 1, -1 ) é um ponto de r, determine:
a) o valor de a;
Como o ponto P = ( 1, -1 ) e pertence à reta r, temos:
b) o coeficiente angular de r.
Como a = 4 , temos:
5) ( UFSCar - SP 2004 ) Os pontos A(3,6), B(1,3) e C(xc, yc) são vértices do triângulo ABC, sendo M (xm, ym) e N(4,5) pontos médios dos lados AB e AC, respectivamente.
a) Calcule a distância entre os pontos M e N.
b) Determine a equação geral da reta suporte do lado BC do triângulo ABC.
Como o ponto N é o ponto médio de AC, temos:
Como os pontos B e C pertencem à BC,temos:
Equação geral da reta suporte do lado BC:
Equação reduzida da reta
Uma reta que corta o eixo y no ponto Q(0,q) e tem uma inclinação m possui equação reduzida dada por:
m: coeficiente angular da reta
q:coeficiente linear da reta
A partir da equação geral da reta ( ax+by+c = 0), podemos obter a equação reduzida desta reta:
Exemplos:
1) A reta r passa pelos pontos A(-3,-4) e B(2,1), determine:
a) a sua equação geral.
b) a sua equação reduzida.
a)
Escolhemos o ponto A parra determinarmos a equação geral da reta,mas poderíamos escolher o ponto B:
Equação geral da reta: 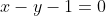
b)
A partir da equação geral, obteremos a equação reduzida da reta:
Equação reduzida da reta: 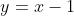
2) (Furg - RS 2003) Dada uma reta r, no plano cartesiano, cuja equação é y= -x + 4, seja s uma reta que não intercepta r e passa pelo ponto (3,-1). Então, a equação da reta s é dada por:
a) y = 2x - 7 b) y = x - 4 c) y = -2x + 5 d) y = -3x + 8 e) y= -x +2
A reta s não intercepta a reta r, então consideraremos r//s: 
Agora, determinaremos a equação da reta s:]
Desta forma, a alternativa correta é a e.
3)( UFRR - RR 2003 ) Considere a reta r, paralela à reta de equação y = 2x - 4, e que contém o ponto (-1,1). As coordenadas do ponto P, interseção da reta r com o eixo y, são:
a) ( -4,0 ) b) ( 3, 0 ) c) ( 0, 0 ) d) ( 0, -4 ) e) ( 0, 3 )
Como a reta r é paralela à reta de equação y = 2x - 4, temos:
Agora determinaremos a equação da reta r:
Agora determinaremos as coordenadas do ponto P. Como ponto P é a interseção da reta r com o eixo y, temos P = ( 0, y).
Desta forma, a alternativa correta é a e.
4) Obtenha a equação reduzida da reta que passa pelo ponto P(2;1) e é paralela à reta r: 2x + y -1 = 0.
A reta é paralela à reta r, então possuem a mesma inclinação:
Agora obteremos a equação reduzida da reta s ( lembremos que ela passa pelo ponto P(2;1)):
Equação segmentária da reta
Ao considerarmos os cortes de uma reta nos eixos x e y respectivamente,podemos obter a equação segmentária desta reta:
p: abscissa do ponto em que a reta corta o eixo x.
q: ordenada do ponto em que a reta corta o eixo y.
Exemplos:
1) (Mackenzie - SP 2003) A reta  forma, no primeiro quadrante, um triângulo de área 6 com os eixos coordenados. O perímetro desse triângulo é:
forma, no primeiro quadrante, um triângulo de área 6 com os eixos coordenados. O perímetro desse triângulo é:
Esboçaremos a equação segmentária abaixo:
A área do triângulo formado com os eixos é dada por:

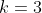
Assim,temos:
O terceiro lado do triângulo obteremos aplicando o Teorema de Pitágoras:

Perímetro do triângulo: 
Desta forma, a alternativa correta é a a.
2) Obtenha a equação segmentária da reta s:

p: interseção da reta no eixo x;
q: interseção da reta no eixo y.
Assim,temos a seguinte equação segmentária para a reta s:

Equações paramétricas da reta
O terceiro lado do triângulo obteremos aplicando o Teorema de Pitágoras:
Perímetro do triângulo: 
Desta forma, a alternativa correta é a a.
2) Obtenha a equação segmentária da reta s:
p: interseção da reta no eixo x;
q: interseção da reta no eixo y.
Assim,temos a seguinte equação segmentária para a reta s:
Podemos estabelecer uma relação entre as coordenadas x e y dos pontos de uma reta e uma variável t. A variável t é um parâmetro.
Dada uma reta r não paralela a algum dos eixos cartesianos, que passa pelos pontos A e B, a relação será estabelecida da seguinte forma:
Equação fundamental da reta r:
Agora relacionaremos cada um dos membros da equação acima à variável t:
Assim, teremos as equações paramétricas da reta:
Exemplos:
1) Ache as coordenadas do ponto de interseção das retas
A partir da equação r, temos:
e
Agora igualaremos as duas equações acima obtidas:
Faremos o mesmo para a reta s:
Agora procuraremos o ponto de interseção das retas r e s:
Ponto de interseção das retas r e s: (2,5).
2) Dadas as equações paramétricas da reta s: x = 5t + 2 e y = 4t, obtenha a sua equação segmentária.
Agora, vamos obter a equação segmentária:
3) Dada a reta r cuja equação geral é x - 2y + 6 = 0, obtenha as equações paramétricas de r.
Primeiramente, obteremos dois pontos aleatórios pertencentes à reta r:
Se x = 0, temos:
Já temos o primeiro ponto: A(0;3). Agora para x = 2, temos:
Temos mais um ponto: B(2;4).
Agora, obteremos as equações paramétricas da reta r:
Equações paramétricas da reta r:
4) Obtenha a equação geral da reta que possui as seguintes equações paramétricas:
A partir das equações paramétricas acima, temos:
Podemos obter a equação geral de dois modos:
Modo 1:
Equação geral: 
Modo 2:
Temos















0 comentários:
Postar um comentário