domingo, 13 de outubro de 2013 , , 0 comentários

Probabilidade–parte II

1. Espaços amostrais equiprováveis

Espaços amostrais equiprováveis são eventos que possuem  as mesmas probabilidades, ou seja,
clip_image003[4]
Exemplos:
1.  Há três crianças participando de um sorteio para ser o ajudante de sala: Ana, Lívia e Davi.
Neste caso, temos o seguinte espaço amostral:
clip_image003[6]
A probabilidade de cada uma  das crianças ser escolhida como ajudante é dada por:
clip_image002
Desta forma, concluímos que estes eventos são equipróváveis.
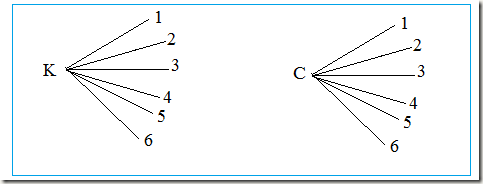
2.  Ao lançarmos uma moeda não-viciada, também temos eventos equiprováveis, pois a probabilidade  de ocorrer cara (K) ou coroa (C) é a mesma:
clip_image002[5]
3.    De um baralho extrai-se, ao acaso, uma carta.
Neste caso, teremos o seguinte espaço amostral:
clip_image003[8]
Onde :  p: carta de paus   c : carta de copas  e: carta de espadas
A: ás
Num baralho comum há 52 cartas.
Qual a probabilidade de a carta extraída ser:
a) um rei de paus;
No baralho há apenas um rei de paus:
clip_image002[9]
clip_image002[13]
b) um valete;
No baralho há 4 valetes:
clip_image002[11]
clip_image002[15]
c) uma carta diferente de uma dama.
O evento de a carta extraída ser uma dama é dado por:
clip_image002[17]
O evento de a carta extraída não ser uma dama é dado por:
clip_image003[10]
clip_image002[19]

2. Probabilidade condicional

Podemos calcular a probabilidade de um evento A, dado que um evento B já ocorreu, ou seja:
clip_image002[1]
Exemplos:
1.  Uma moeda e um dado são lançados juntos. Qual a probabilidade de:
a) obtermos cara na face superior, uma vez  que o número da face superior do dado é par;
No lançamento do dado e da moeda juntos, teríamos as seguintes possibilidades de eventos:
image
clip_image003
clip_image002[3]
clip_image004
clip_image002[7]
clip_image002[9]
clip_image004[6]
clip_image006
2. Dois dados são lançados juntos. Qual a probabilidade de a soma dos pontos nos dois dados ser igual a 7, uma vez que o número observado no dado 1 é um múltiplo de 2.
No lançamento dos dados juntos, teríamos as seguintes possibilidades de eventos:
image
clip_image003[7]
clip_image002[11]
clip_image004[8]
clip_image006[5]
clip_image008
clip_image010
clip_image012
clip_image014
clip_image016
3.  Formaremos uma comissão de 3 pessoas realizando uma escolha ao acaso entre 6 pessoas: Ana, Beatriz, Maria, José, João e Pedro. Se Maria  e João não fizerem  parte da comissão, qual a probabilidade de Ana participar desta comissão?
Neste caso, o espaço amostral é determinado pela combinação de 6 pessoas, tomadas 3 a 3:
clip_image003[11]
clip_image002[17]
Como João e Maria não farão parte da comissão, a escolha será feita entre as quatro pessoas restantes:
clip_image002[15]
clip_image002[27]
clip_image005
clip_image007
clip_image002[23]
clip_image002[29]
clip_image004[14]
clip_image006[7]
Postado por Lislene às 13:32
segunda-feira, 7 de outubro de 2013 , , 0 comentários

Probabilidade–parte I

1. Espaço amostral
Espaço amostral : conjunto de todos os resultados possiveis de um certo experimento aleatório.
clip_image004
Exemplos:
a) Lançamento de um dado
clip_image003
b) Um casal planeja ter dois filhos. Vejamos a seqüência de sexo dos dois filhos.
clip_image003[5]
2. Evento
Evento: é um subconjunto do espaço amostral.
Exemplos:
a) Um dado é lançado uma vez e é observada a sua face superior. Descreva os eventos:
a.1.  a face superior é um número par
clip_image002 
a.2. a face superior é um número ímpar
clip_image002[5]
a.3. a face superior é um multiplo de 2 ou de 3
clip_image002[7]
b) Uma moeda e um dado são lançados. Descreva os eventos:
Usaremos as seguintes notações : C – coroa e K – cara.
b.1. ocorre coroa
clip_image002[9]
b.2. ocorre número ímpar
clip_image002[11]
b.3.  A U B -  ocorre coroa ou número ímpar
clip_image002[13]
b.3. clip_image002[15] - ocorre coroa e número ímpar
clip_image002[17]
b.4. clip_image002[21] - não ocorre coroa
Neste caso, temos um evento complementar, ou seja, o espaço amostral menos o evento. Assim temos:
clip_image003[7]
clip_image003[9]
3. Probabilidade
A probabilidade de um certo evento é a chance do mesmo ocorrer.

Exemplos:
a) Numa urna há 3 bolas azuis e 7 bolas amarelas. Ao retirar-se uma bola, qual a probabilidade dela ser amarela?
clip_image002[7]
clip_image002[1]
b) Uma urna contém 50 bolinhas, numeradas de 1  a 50. Uma bolinha é retirada, qual a probabilidade de :
b.1. o número da bolinha ser um míltiplo de 4;
clip_image002[9]
clip_image002[11]
clip_image002[13]
b.2.  o número da bolinha não ser um múltiplo de 4;
clip_image002[29]
clip_image004[9]
clip_image006[12]
clip_image002[31]
clip_image004[11]
clip_image006[14]

b.3.  o número da bolinha ser um múltiplo de 5 e de 4;
clip_image002[21]
clip_image004[1]
clip_image006
clip_image002[15]
clip_image002[17]
clip_image002[19]

clip_image002[23]
clip_image004[3]
clip_image006[6]
b.4.  o número da bolinha ser um múltiplo de 5 ou de 4;
clip_image002[25]
clip_image004[5]
clip_image006[8]
clip_image008
clip_image010
clip_image012
clip_image002[27]
clip_image004[7]
clip_image006[10]
clip_image008[5]
clip_image010[5]
clip_image012[5]
clip_image014
c) Se A, B e C são eventos tais que :
clip_image002[49] clip_image004[15] clip_image006[18] clip_image008[9] clip_image010[9]clip_image012[9]clip_image014[6]

Determine:
c.1.
clip_image002[35]
clip_image002[41]
c.2.
clip_image002[37]
clip_image002[45]
c.3.
clip_image002[39]

clip_image002[47]
clip_image002[51]
Postado por Lislene às 14:32
Assinar: Postagens (Atom)
 
;