Operações entre matrizes
Podemos obter a soma de duas matrizes de mesma ordem m x n, somando-se os elementos correspondentes de cada uma das matrizes. Ou seja, dadas duas matrizes A e B de mesma ordem, sua soma será dada por uma matriz C, na qual cada elemento será dado por:
Exemplos:
1) Dadas
2) Seja C uma matriz quadrada de ordem 2, a soma das matrizes A e B dadas abaixo. Calcule a soma
3) FEI - SP Se as matrizes  e
e  estão assim definidas
estão assim definidas
Desta forma, a alternativa correta é a d.
1.1.Propriedades da Adição de matrizes
Propriedade Comutativa: 
Propriedade Associativa: 
Elemento Neutro: 
Elemento Oposto: 
Cancelamento: 
2.Subtração de matrizes
Podemos obter a diferença de duas matrizes de mesma ordem m x n, subtraindo-se os elementos correspondentes de cada uma das matrizes. Ou seja, dadas duas matrizes A e B de mesma ordem, sua diferença será dada por uma matriz C, na qual cada elemento será dado por:
Exemplos:
1) Dadas  e
e  , calcule A-B.
, calcule A-B.
2) Dadas as matrizes A e B, calcule A-B.
3) Determine os valores de x e y, sabendo que:
3.Multiplicação de um número real por uma matriz
Dada uma matriz  , podemos multiplicá-la por um número real k, obtendo-se uma nova matriz, ou seja, multiplicaremos cada elemento da matriz A por k.
, podemos multiplicá-la por um número real k, obtendo-se uma nova matriz, ou seja, multiplicaremos cada elemento da matriz A por k.
Exemplos:
1)
2)
3) FACEAG - SP Dadas as matrizes
Desta forma, a alternativa correta e a c.
4) Resolva o sistema e encontre as matrizes X e Y:
31.Propriedades
Sendo A e B duas matrizes quaisquer do mesmo tipo e a e b dois números reais quaisquer, o produto de um número por uma matriz possui as seguintes propriedades:
4. Equações matriciais
Equações matriciais são equações que possuem matrizes como incógnitas.
Exemplos:
1) Dadas a matrizes A e B, obtenha a matriz X tal que X - A = B.
2) UFRN - RN A solução da equação matricial
a) maior que -1 b) menor que -1 c) maior que 1 d) entre -1 e 1 e) entre 0 e 3
Desta forma, a alternativa correta é a b.
3) Determine as matrizes X e Y:
5. Multiplicação de matrizes
A multiplicação de duas matrizes só será possível quando tivermos o número de colunas da matriz A igual ao número de linhas da matriz B:
Assim, o produto da matriz A pela matriz B será dado por:
Basicamente, o produto de duas matrizes é obtido multiplicando-se as linhas de uma matriz pelas colunas da segunda matriz, conforme veremos nos exemplos a seguir.
Exemplos:
1) Dadas as matrizes A e B, calcule A.B.
Neste caso, não é possível realizarmos a multiplicação, pois o número de colunas da matriz A (2 colunas) é diferente do número de linhas da matriz B(3 linhas).
2) Dadas as matrizes A e B, calcule A.B.
Observemos que :
3) Determine o produto das matrizes abaixo:
4) Fuvest - SP Considere as matrizes
O elemento  é:
é:
a) -112 b)-18 c)-56 d) 112 e) não existe
Como a matriz A é 4x7 e a matriz B é 7x9, teremos:
Logo,  não existe.
não existe.
A alternativa correta é a e.
5) UFC - CE 2004
O valor de a para que a igualdade matricial
a) 1 b) 2 c) 0 d) -2 e) -1
A alternativa correta é a b.
6)Fatec - SP 2003 Seja a matriz
É verdade que a+b é igual a :
a) 0 b) 1 c) 9 d) -1 e) -9
Logo a alternativa correta é a b.
7) PUC-RS Sabendo que  , o valor de y.z é:
, o valor de y.z é:
a) -6 b) -5 c) -1 d) 5 e) 6
Resolveremos o sistema acima pelo método da substituição:
Agora resolveremos o outro sistema pelo método da substituição:
Sendo assim, teremos:
Logo, a alternativa correta é a d.
8) UFSCar - SP 2002 - Seja a matriz  , tal que
, tal que  .
.
a) Escreva M na forma matricial.
b) Sendo  a matriz transposta de M, calcule o produto
a matriz transposta de M, calcule o produto  .
.
5.1. Propriedades da multiplicação de matrizes
5.1.1. A multiplicação de matrizes não é comutativa:
Observemos que  .
.
5.1.2. A propriedade do cancelamento não é válida na multiplicação de matrizes:
5.1.3. A propriedade do anulamento não é válida na multiplicação de matrizes:
Exemplo:
5.1.4. Na multiplicação de matrizes são válidas as propriedades associativa e distributiva:
(1)
Exemplo:
Observemos que  .
.
(2)
Desta forma, concluímos que :
(3)
Desta forma, concluímos que :
6. Matriz inversa
Uma matriz A é inversível se existir uma matriz 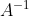 , tal que:
, tal que:
Exemplos:
1)UFRGS-RS A inversa da matriz abaixo é:
Resolvendo o sistema pelo método de substituição, teremos:
Da mesma forma, resolveremos o outro sistema:
A alternativa correta é a a.
2) Vunesp - SP Seja  a matriz real 2x2 definida por :
a matriz real 2x2 definida por :
Calcule 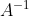 .
.
Resolvendo os sistemas pelo método de adição, teremos:
















































- Follow Us on Twitter!
- "Join Us on Facebook!
- RSS
Contato