Radiciação - Parte II

Racionalização de denominadores

A operação de racionalização consiste na transformação de um número irracional em um número racional. No caso de racionalização de denominadores trata-se da eliminação do radical no denominador.

Em algumas situações, basta multiplicarmos o numerador e o denominador por um fator de racionalização, conforme veremos abaixo.

1. Denominadores do tipo 

Neste caso, para efetuarmos a racionalização de denominadores, só precisaremos multiplicar o numerador e o denominador por  ( fator de racionalização), pois assim eliminaremos o radical que estiver no denominador.

Exemplos:

1)

2)

3)

4)

5)

6)

7) Simplifique as expressões abaixo:

a) 

b)

2. Denominadores do tipo 

Neste caso, para efetuarmos a racionalização de denominadores, só precisaremos multiplicar o numerador e o denominador pelo conjugado do denominador,pois assim eliminaremos o radical que estiver no denominador.

* Observe que:

- Se o denominador for ,  o seu conjugado será ;

- Se o denominador for , o seu conjugado será .

Exemplos:

1)

2)

3)

4)

5)

6) Determine o valor de x que satisfaça a equação abaixo:

             

7) PUC - SP

Se       e  , então x+y é igual a:

                                  

Desta forma, a alternativa correta é a a.

8)  Uepi - PI 2003

A expressão  , na forma racionalizada, é igual a :

                                           

Sendo assim, temos:

Desta forma, a alternativa correta é a a.

9) UEPB-PB 2004

Calculando o valor de  obtemos:

                                         

Primeiramente, vamos calcular a fração geratriz  desta dízima periódica :

                    

          

A fração geratriz que procuramos é:  

Desta forma, a alternativa correta é a a.

10) Ufor- CE 2002

Se        ,    e   , então:

                              

:

*Observemos que:

  

Desta forma, concluimos que 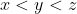,  então a alternativa correta é a a.