Equações logarítmicas

Uma equação logarítmica sempre possui incógnita no logaritmando, na base o logaritmo ou no logaritmo.

Exemplos:

$1)\log_{4}\left ( x+3 \right )=2$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x+3> 0\Rightarrow x> -3$

Agora vamos resolver a equação:

$\log_{4}\left ( x+3 \right )=2$

$4^{2}=x+3\Rightarrow 16=x+3\Rightarrow x=13$

Observemos que x=13, satisfaz a condição de existência (x>-3).

$S=\left \{ 13 \right \}$

$2) \log_{y}81=4$

Primeiramente vamos determinar a condição de existência do logaritmo:

$y> 0$ e $y\neq 1$

Agora vamos resolver a equação:

$\log_{y}81=4\Rightarrow y^{4}=81\Rightarrow y^{4}=3^{4}\Rightarrow y=3$

y = 3 satisfaz a condição de existência , logo é a solução da equação.

$S=\left \{ 3 \right \}$

$3) \log_{5}\left ( x^{2} -4\right )=\log_{5}\left ( 4x \right )$

Primeiramente vamos determinar a condição de existência do logaritmo:

(I ) $x^{2}-4> 0$ e ( II ) $4x> 0\Rightarrow x> 0$

Há duas formas de fazermos a verificação da condição de existência:

* (A)Encontrando a intercessão entre as condições ( I ) e ( II ):

$(I) x^{2}-4> 0$

$x^{2}-4=0\Rightarrow x=\pm2$

A partir do estudo de sinal esboçado no gráfico acima, teremos $x^{2}-4> 0\Leftrightarrow x< -2$ ou $x> 2$ :

$(II)x>0$

Agora encontraremos a intersecção entre as condições ( I ) e ( II ):

Sendo assim, a condição de existência é: $\left \{ x\epsilon R/x>2 \right \}$ .

*(B) Fazendo as verificações diretamente nas condições ( I ) e ( II ).

Faremos este tipo de verificação,logo após solucionarmos a equação!

Agora vamos resolver a equação:

$\log_{5}\left ( x^{2}-4 \right )=\log_{5}\left ( 4x \right )$

Como os logaritmos possuem a mesma base, poderemos igualar os logaritmandos:

$x^{2}-4 =4x$

$x^{2}-4x -4=0$

$x_{1}=2+2\sqrt{2}$ e $x_{2}=2-2\sqrt{2}$

Verificação na forma (A):

$x_{1}=2+2\sqrt{2}$ satisfaz a condição de existência $\left ( x> 2 \right )$ .

$x_{2}=2-2\sqrt{2}$ não satisfaz a condição de existência $\left ( x> 2 \right )$ .

Verificação na forma (B):

( I ) $x^{2}-4> 0$

Para $x_{1}=2+2\sqrt{2}$ , temos:

$\left ( 2+2\sqrt{2} \right )^{2}-4> 0\Rightarrow \left (2 ^{2}+2.2.2\sqrt{2}+\left ( 2\sqrt{2} \right )^{2}-4 \right )>0$ $\Rightarrow 8\sqrt{2}+8> 0 (V)$

$\left ( 2-2\sqrt{2} \right )^{2}-4> 0\Rightarrow \left (2 ^{2}-2.2.2\sqrt{2}+\left ( -2\sqrt{2} \right )^{2}-4 \right )>0$ $\Rightarrow -8\sqrt{2}+8> 0 (F)$

$S=\left \{ 2+2\sqrt{2} \right \}$

$4)\log_{4}\left ( 3x-5 \right )=\log_{4}40$

Primeiramente vamos determinar a condição de existência do logaritmo:

$3x-5 > 0\Rightarrow x> \frac{5}{3}$

Agora vamos resolver a equação:

$\log_{4}\left ( 3x-5 \right )=\log_{4}40$

$3x-5=40$

$3x=45\Rightarrow x=15$ ( satisfaz a condição de existência )

$S=\left \{ 15 \right \}$

$5) \log_{}\left ( x^{2}-3x-10 \right )=\log_{}\left ( 2-2x \right )$

Primeiramente vamos determinar a condição de existência do logaritmo:

$(I) x^{2}-3x-10> 0$ e $(II) 2-2x> 0$

* Observação: Podemos optar por uma das duas formas de verificação das condições de existência apresentados no exercício 3!

Neste exercício usarei a forma de verificação (A)!

$(I) x^{2}-3x-10>0$

Faremos o estudo de sinal da inequação acima:

$x^{2}-3x-10=0\Rightarrow x_{1}=-2$ e $x_{2}=5$ .

A partir do estudo de sinal esboçado no gráfico acima, teremos $x^{2}-3x-10> 0$ $\Leftrightarrow x< -2$ ou $x> 5$ :

$(II) 2-2x> 0\Rightarrow x<1$

Agora encontraremos a intersecção entre as condições ( I ) e ( II ):

Sendo assim, a condição de existência é: $\left \{ x\epsilon R/x<-2 \right \}$

Agora vamos resolver a equação:

$\log_{}\left ( x^2-3x-10 \right )=\log_{}\left ( 2-2x \right )$

$x^2-3x-10= 2-2x$

$x^2-x-12=0$

$x_{1}=-3$ (satisfaz a condição de existência) e $x_{2}=4$ (não satisfaz a condição de existência).

$S=\left \{ -3 \right \}$

$6) \log_{9}\left ( x^{2}+3x-1 \right )=1$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x^{2}+3x-1> 0$

* Observação: Podemos optar por uma das duas formas de verificação das condições de existência apresentados no exercício 3!

Neste exercício usarei a forma de verificação (B)!

Agora vamos resolver a equação:

$\log_{9}\left ( x^{2}+3x-1 \right )=1$

$9^{1}=x^{2}+3x-1\Rightarrow x^{2}+3x-10=0$

$x_{1}=-5$ Verificação:

$x^{2}+3x-1> 0$

$(-5)^{2}+3.(-5)-1> 0\Rightarrow 9> 0(V)$

$x_{2}=2$

Verificação:

$x^{2}+3x-1> 0$

$2^{2}+3.2-1> 0\Rightarrow 9> 0(V)$

Ambas as soluções satisfazem a condição de existência, então temos:

$S=\left \{ -5;2 \right \}$

$7)\left ( \log_{3}x \right )^{2}-\log_{3}x=2$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x> 0$

Agora vamos resolver a equação:

$\left ( \log_{3}x \right )^{2}-\log_{3}x=2$

Usaremos uma variável auxiliar $k=\log_{3}x$ , então a equação será dada por:

$k^{2}-k=2$ $\Rightarrow k^{2}-k-2=0$

$k_{1}=2$ e $k_{2}=-1$

Assim, teremos:

$\log_{3}x=2$ e $\log_{3}x=-1$ .

$\log_{3}x=2\Rightarrow 3^{2}=x\Rightarrow x=9$ ( satisfaz a condição de existência).

$\log_{3}x=-1\Rightarrow 3^{-1}=x\Rightarrow x=\frac{1}{3}$ ( satisfaz a condição de existência).

$S=\left \{ \frac{1}{3};9 \right \}$

$8)\log_{3}\left ( \log_{2}x \right )=1$

Primeiramente vamos determinar a condição de existência do logaritmo:

$( I )\log_{2}x>0$ e $( II )x>0$

Agora vamos resolver a equação:

$\log_{3}\left ( \log_{2}x \right )=1$

$3^{1}=\log_{2}x\Rightarrow \log_{2}x=3$ ( satisfaz a condição (I) )

$\log_{2}x=3\Rightarrow 2^{3}=x\Rightarrow x=8$ ( satisfaz a condição (II) )

$S=\left \{ 8 \right \}$

$9)\frac{1}{5-\log_{}x}+\frac{2}{1+\log_{}x}=1$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x> 0$

Usaremos a variável auxiliar $k=\log_{}x:$

$\frac{1}{5-\log_{}x}+\frac{2}{1+\log_{}x}=1$

$\frac{1}{5-k}+\frac{2}{1+k}=1$

$\frac{1.\left ( 1+k \right )+2.\left ( 5-k \right )}{\left ( 5-k \right ).\left ( 1+k \right )}=\frac{\left ( 5-k \right )\left ( 1+k \right )}{\left ( 5-k \right ).(1+k)}$

$1+k+10-2k=-k^{2}+4k+5$

$k^{2}-5k+6=0$

$k_{1}=2$ e $k_{2}=3$

Assim, teremos:

$\log_{}x=2\Rightarrow 10^{2}=x\Rightarrow x=100$ ( satisfaz a condição de existência ).

$\log_{}x=3\Rightarrow 10^{3}=x\Rightarrow x=1000$ ( satisfaz a condição de existência )

$S=\left \{ 100;1000 \right \}$

$10)\log_{x}\left ( 3x^{2}-13x+15 \right )=2$

Primeiramente vamos determinar a condição de existência do logaritmo:

$(I)x> 0$ e $(II)3x^{2}-13x+15> 0$

Agora vamos resolver a equação:

$\log_{x}\left ( 3x^{2}-13x+15 \right )=2$

$x^{2}=3x^{2}-13x+15$

$2x^{2}-13x+15=0$

$x_{1}=5$ e $x_{2}=\frac{3}{2}$

Verificação:

$x_{1}=5:$ (satisfaz a condição ( I ));

$3x^{2}-13x+15> 0$ :

$3.5^{2}-13.5+15> 0\Rightarrow 25>0(V)$ (satisfaz a condição (II)).

$x_{2}=\frac{3}{2}:$ (satisfaz a condição (I));

$3x^{2}-13x+15> 0$ :

$3.\left ( \frac{3}{2} \right )^{2}-13.\left ( \frac{3}{2} \right )+15> 0\Rightarrow\frac{9}{4} >0(V)$ (satisfaz a condição (II)).

$S=\left \{ \frac{3}{2};5 \right \}$

$11)\log_{\sqrt{x}}\left ( 2x^{2}+5x+6 \right )=4$

Primeiramente vamos determinar a condição de existência do logaritmo:

$( I))2x^{2}+5x+6> 0$

$( II))\sqrt{x}> 0$ e $\sqrt{x}> 1$ $\Rightarrow \left ( \sqrt{x} \right )^{2}> 0^{2}\Rightarrow x> 0$ e $\left ( \sqrt{x} \right )^{2}> 1^{2}\Rightarrow x> 1$

$(II)x>0$ e $x>1$ :

$\log_{\sqrt{x}}\left ( 2x^{2}+5x+6 \right )=4$

$\left ( \sqrt{x} \right )^{4}=2x^{2}+5x+6$

$\left (x^{\frac{1}{2}} \right )^{4}=2x^{2}+5x+6$

$x^{\frac{1}{2}.4}=2x^{2}+5x+6$

$x^{2}=2x^{2}+5x+6$

$x^{2}+5x+6=0$

$x_{1}=-3$ e $x_{2}=-2$ :

Verificação:

$x_{1}=-3:$ (não satisfaz a condição (II));

$2.\left ( -3 \right )^{2}+5.(-3)+6> 0\Rightarrow 9>0(V)$ (satisfaz a condição (I))

$x_{2}=-2:$ (satisfaz a condição (II));

$2.\left ( -2 \right )^{2}+5.(-2)+6> 0\Rightarrow 4>0(V)$ (satisfaz a condição (I)).

$S=\varnothing$

12) (FGV - SP) A equação logarítmica $\log_{2}\left ( x+1 \right )+\log_{2}\left ( x-1 \right )=3$ admite:

a) uma única raiz irracional; b)duas raízes opostas; c) duas raízes cujo produto é -4;

d) uma única raiz e negativa; e) uma única raiz e maior do que 2.

Primeiramente vamos determinar a condição de existência do logaritmo:

$(I))x+1> 0\Rightarrow x>-1$ e $(II))x-1> 0\Rightarrow x>1$ :

Condição de existência: $\left \{ x\epsilon R/x> 1 \right \}$ .

Agora resolveremos a equação:

$\log_{2}\left ( x+1 \right )+\log_{2}\left ( x-1 \right )=3$

$\log_{2}\left ( x+1 \right ).(x-1)=3$

$2^{3}=\left ( x+1 \right ).\left ( x-1 \right )\Rightarrow x^{2}-1=8\Rightarrow x^{2}=9\Rightarrow x=\pm 3$

$x_{1}=-3$ (não satisfaz a condição de existência)

$x_{2}=3$ (satisfaz a condição de existência)

$S=\left \{ 3 \right \}$

13) (Cesgranrio - RJ) Se $\log_{}x$ representa o logaritmo decimal do número positivo x, a soma das raízes de $\left (\log_{}x \right )^{2}-\log_{}x^{2}=0$ é:

$a)-1$ $b)1$ $c)20$ $d)100$ $e)101$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x> 0$

Agora vamos resolver a equação, usando a variável auxiliar $k=\log_{}x$ :

$\left (\log_{}x \right )^{2}-\log_{}x^{2}=0$

$\left ( \log_{}x \right )^{2}-2.\log_{}x=0$

$k^{2}-2k=0\Rightarrow k.\left ( k-2 \right )=0\Rightarrow k=0$ e $k=2$ .

Sendo assim, teremos:

$\log_{}x=0$ e $\log_{}x=2$ .

$\log_{}x=0\Rightarrow 10^{0}=x\Rightarrow x=1$ (satisfaz a condição de existência)

$\log_{}x=2\Rightarrow 10^{2}=x\Rightarrow x=100$ (satisfaz a condição de existência)

$S=\left \{ 1;100 \right \}$

Soma das raízes: 101.

Desta forma, a alternativa correta é a e.

14) (FGV) O valor de x que satisfaz a equação $\log_{}\left ( 2x+7 \right )=\log_{}2x+\log_{}7$ é um número:

a) menor que 1/2 b) entre 1/2 e 1 c) entre 1 e 3/2 d) entre 3/2 e 2 e) maior que 2

Primeiramente vamos determinar a condição de existência do logaritmo:

$(I)2x+7>0\Rightarrow x>\frac{-7}{2}$

$(II)2x>0\Rightarrow x>0$

Encontraremos a intersecção entre (I) e (II) para determinarmos a condição de existência:

Condição de existência: $\left \{ x\epsilon R/x>0 \right \}$ .

Agora resolveremos a equação:

$\log_{}\left ( 2x+7 \right )=\log_{}2x+\log_{}7$

$\log_{}\left ( 2x+7 \right )=\log_{}\left ( 2x.7 \right )$

$\log_{}\left ( 2x+7 \right )=\log_{}\left ( 14x\right )$

$2x+7 = 14x$

$12x=7$

$x=\frac{7}{12}$ ( satisfaz a condição de existência) e está entre 1/2 e 1.

Desta forma, a alternativa correta é a b.

13) (FGV) a) Resolva a equação $\log_{}\left ( x-2 \right )+\log_{}\left ( x+2 \right )=2$ .

b) Quais as raízes da equação $x^{\log_{}x}=100x$ ?

Primeiramente vamos determinar a condição de existência do logaritmo:

$(I)x-2>0\Rightarrow x>2$ e $(II)x+2>0\Rightarrow x>-2$

Encontraremos a intersecção entre ( I ) e ( II ) para determinarmos a condição de existência:

Condição de existência: $\left \{ x\epsilon R/x>2 \right \}$ .

Agora resolveremos a equação:

$\log_{}\left ( x-2 \right )+\log_{}\left ( x+2 \right )=2$

$\log_{}\left ( x-2 \right )\left ( x+2 \right )=2$

$10^{2}=\left ( x-2 \right )\left ( x+2 \right )$

$100=x^{2}-4$

$x^{2}=104$

$x=\pm 2\sqrt{26}$

$x_{1}=-2\sqrt{26}$ ( não satisfaz a condição de existência )

$x_{2}=2\sqrt{26}$ ( satisfaz a condição de existência )

$S=\left \{ 2\sqrt{26} \right \}$

Primeiramente vamos determinar a condição de existência do logaritmo:

$x>0$

Agora procuraremos as raízes da equação:

$x^{\log_{}x}=100x$

$\log_{}\left ( x^{\log_{}x} \right )=\log_{}\left ( 100x \right )$

$\log_{}x.\left ( \log_{} x\right )=\log_{}100+\log_{}x$

$\left ( \log_{} x\right )^{2}=\log_{}10^{2}+\log_{}x$

$\left ( \log_{} x\right )^{2}=2\log_{}10+\log_{}x$

$\left ( \log_{} x\right )^{2}=2+\log_{}x$

$\left ( \log_{} x\right )^{2}-\log_{}x-2=0$

Usaremos a variável auxiliar $k=\log_{}x$ :

$k^{2}-k-2=0$

$k_{1}=-1$ e $k_{2}=2$ .

Assim, teremos:

$\log_{}x=-1$ e $\log_{}x=2$ .

$\log_{}x=-1\Rightarrow 10^{-1}=x\Rightarrow x=\frac{1}{10}$ ( satisfaz a condição de existência)

$\log_{}x=2\Rightarrow 10^{2}=x\Rightarrow x=100$ (satisfaz a condição de existência)

$S=\left \{ \frac{1}{10};100 \right \}$

14) (IBMEC - 2003) O número de soluções de $e^{\ln{}x}=x^{2}$ em R é:

a) 0 b) 4 c) 3 d) 2 e)1

Condição de existência: $x>0$

$e^{ln_{}x}=x^{2}$

$x=x^{2}$

$x^{2}-x=0\Rightarrow x.\left ( x-1 \right )=0$

$x_{1}=0$ (não satisfaz a condição de existência)

$x_{2}=1$ ( satisfaz a condição de existência)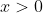

A equação tem uma solução real.

Desta fora, a alternativa correta é a e.

15) (UFU - MG 2003) Supondo que o determinante da matriz $\begin{pmatrix} -1 & 1\\ -\log_{3}x &3^{4} \end{pmatrix}$ seja igual a -1, então o valor de $\log_{9}x$ será igual a :

a) 80 b) 40 c) 82 d) 41

$\begin{vmatrix} -1 & 1\\ -\log_{3}x &3^{4} \end{vmatrix}=-1$

$\left ( -1 \right ).3^{4}-\left ( -\log_{3}x.1 \right )=-1$

$-81+\log_{3}x=-1$

$\log_{3}x=80$

Condição de existência: $x> 0$

$\log_{9}x=\frac{\log_{3}x}{\log_{3}9}=\frac{\log_{3}x}{\log_{3}3^{2}}=\frac{\log_{3}x}{2}=\frac{80}{2}=40$ (satisfaz a condição de existência)

$S=\left \{ 40 \right \}$

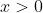
Desta forma, a altenativa correta é a b.

16) ( PUC - RS 2003 ) O conjunto solução da equação $\ln_{}\left ( \frac{1}{x} \right )+\ln_{}\left ( 2x^{3} \right )=\ln_{}3$ é:

$a)\left \{ \frac{-\sqrt{3}}{2},\frac{\sqrt{3}}{2} \right \}$ $b)\left \{ -\sqrt{\frac{3}{2}}, \sqrt{\frac{3}{2}} \right \}$ $c)\left \{ \sqrt{\frac{3}{2}} \right \}$ $d)\left \{ -1,1 \right \}$

$\ln_{}\left ( \frac{1}{x} \right )+\ln_{}\left ( 2x^{3} \right )=\ln_{}3$

$\log_{e}\left ( x^{-1} \right )+\log_{e}\left ( 2x^{3} \right )=\log_{e}3$

$\log_{e}(x^{-1}.2x^{3}) =\log_{e}3$

$\log_{e}(2x^{3-1}) =\log_{e}3$

$\log_{e}(2x^{2}) =\log_{e}3$

Condição de existência: $2x^{2}> 0\Rightarrow x> 0$

$2x^{2} =3\Rightarrow x=\pm \sqrt{\frac{3}{2}}$

$x_{1}=-\sqrt{\frac{3}{2}}$ (não satisfaz a condição de existência)

$x_{2}=\sqrt{\frac{3}{2}}$ (satisfaz a condição de existência)

$S=\left \{ \sqrt{\frac{3}{2}} \right \}$

Desta forma, a alternativa correta é a c.

17) ( UFRR - RR 2003) O valor de x que resolve a equação $\log_{3}\left ( x-\log_{2}4 \right )=2$ é:

a) múltiplo de 2 b) divisível por 3 c) um valor não-inteiro d) um quadrado perfeito

e) um número primo

$\log_{3}\left ( x-\log_{2}4 \right )=2$

Condição de existência:

$x-\log_{2}4 > 0$

$x-\log_{2}2^{2} > 0$

$x-2\log_{2}2 > 0$

$x-2 > 0\Rightarrow x> 2$

Agora resolveremos a equação:

$\log_{3}\left ( x-\log_{2} 4\right )=2$

$3^{2}=x-\log_{2}4$

$9=x-2\Rightarrow x=11$ (satisfaz a condição de existência)

Desta forma, o valor de x ( x= 11 ) é um número primo. E a alternativa correta é a e.

18) (FMTM - MG 2004) O número de pares (a,b), com a e b inteiros e maiores que 1, que satisfazem a equação

$2\log_{}a+\log_{}b=\log_{}108$ é:

a) 1 b) 2 c) 3 d) 4 e) 5

$2\log_{}a+\log_{}b=\log_{}108$

$\log_{}a^{2}+\log_{}b=\log_{}108$

$\log_{}\left ( a^{2}.b \right )=\log_{}108$

$\log_{}\left ( a^{2}.b \right )=\log_{}\left (2 ^{2}.3^{3} \right )$

Assim, teremos:

$a^{2}=2^{2}\Rightarrow a=2$ e $b=3^{3}=27$ : $\left ( a,b \right )=\left ( 2,27 \right )$

$a^{2}=3^{3}\Rightarrow a=\pm \sqrt{3^{3}}=\pm \sqrt{3^{2}.3}=\pm 3\sqrt{3}$

e $b=2^{2}=4$ :

$\left ( a,b \right )=\left ( 3\sqrt{3},4 \right )$ $\left ( a,b \right )=\left ( -3\sqrt{3},4 \right )$

Assim, temos 3 pares (a,b).

Desta forma, a alternativa correta e a c.

19) ( Mackenzie -SP 2003) Se $\log_{3}\left ( 3x \right )-\log_{9}x-\log_{3}x=2$ , então $\log_{\frac{1}{3}}\left ( 3x \right )$ vale:

a) -1 b) -1/3 c) 1/9 d) 1/3 e) 1

Observemos que:

$\log_{3}\left ( 3x \right )=\log_{3}3+\log_{3}x=1+\log_{3}x$

$\log_{9}\left ( x \right )=\frac{\log_{3}x}{\log_{3}9}=\frac{\log_{3}x}{\log_{3}3^{2}}=\frac{\log_{3}x}{2.\log_{3}3}=\frac{\log_{3}x}{2}$

Assim, teremos:

$\log_{3}\left ( 3x \right )-\log_{9}x-\log_{3}x=2$

$\left ( 1+\log_{3}x \right )-\frac{\log_{3}x}{2}-\log_{3}x=2$

$\frac{2(1+\log_{3}x)-\log_{3}x-2\log_{3}x}{2}=\frac{4}{2}$

$2+2\log_{3}x-\log_{3}x-2\log_{3}x=4$

$2-\log_{3}x=4$

$-\log_{3}x=2$

Condição de existência: $x> 0$

$-\log_{3}x=2\Rightarrow \log_{3}x^{-1}=2\Rightarrow 3^{2}=x^{-1}\Rightarrow 9=\frac{1}{x}\Rightarrow x=\frac{1}{9}$

$x=\frac{1}{9}$ (satisfaz a condição de existência)

$S=\left \{ \frac{1}{9} \right \}$

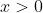
Desta forma, a alternativa correta é a c.

Bloglis

Equações logarítmicas

Equações logarítmicas

0 comentários:

Postar um comentário

Labels

Pages

Blog archive

Latest Tweets