Logaritmos - Introdução

1. Definição

Sejam a e b dois números reais positivos $\left ( a>0 ,a\neq 1\right )$ , $\left ( b>0 \right )$ , denomina-se logaritmo de b na base a o expoente que colocado à base a resulte em b:

$\log_{a}b=x$

a: base, b: logaritmando e x: logaritmo.

Exemplos:

$1) \log_{2}32=5$

Raciocínio:

$\log_{2}32=x\Leftrightarrow 2^{x}=32$

Devemos decompor 32 em fatores primos:

$32=2^{5}$

Assim, teremos:

$2^{x}=32\Rightarrow 2^{x}=2^{5}\Rightarrow x=5$

$2) \log_{10}100=2$

Raciocínio:

$\log_{10}100=x\Rightarrow10 ^{x}=100$

Não nos esqueçamos de decompor 100 em fatores primos:

$100=2^{2}.5^{2}=\left ( 2.5 \right )^{2}=10^{2}$

Assim, teremos:

$10^{x}=10^{2}\Rightarrow x=2$

$3) \log_{10}0,01=-2$

Raciocínio:

$\log_{10}0,01=x\Rightarrow 10^{x}=0,01\Rightarrow 10^{x}=10^{-2}\Rightarrow x=-2$

$4)\log_{8}2=\frac{1}{3}$

Raciocínio:

$\log_{8}2=x\Rightarrow 8^{x}=2\Rightarrow\left ( 2^{3} \right )^{x}=2^{1}\Rightarrow 3x=1\Rightarrow x=\frac{1}{3}$

$5)\log_{3}\frac{1}{27}=-3$

Raciocínio:

$\log_{3}\frac{1}{27}=x\Rightarrow 3^{x}=\frac{1}{27}\Rightarrow 3^{x}=3^{-3}\Rightarrow x=-3$

$6)\log_{2}\sqrt{8}=\frac{3}{2}$

Raciocínio:

$\log_{2}\sqrt{8}=x\Rightarrow 2^{x}=\sqrt{8}\Rightarrow 2^{x}=2^{\frac{3}{2}}\Rightarrow x=\frac{3}{2}$

$7)\log_{\sqrt[3]{7}}343=9$

Raciocínio:

$\log_{\sqrt[3]{7}}343=x\Rightarrow \left ( \sqrt[3]{7} \right )^{x}=343\Rightarrow \left (7^{\frac{1}{3}} \right )^{x}=7^{3}\Rightarrow 7^{\frac{x}{3}}=7^{3}\Rightarrow x=9$

$8) \log_{\sqrt{8}}\sqrt{32}=\frac{5}{3}$

Raciocínio:

$\log_{\sqrt{8}}\sqrt{32}=x\Rightarrow \left ( \sqrt{8} \right )^{x}=\sqrt{32}\Rightarrow \left (2^{\frac{3}{2}} \right )^{x}=2^{\frac{5}{2}}\Rightarrow \frac{3x}{2}=\frac{5}{2}\Rightarrow x=\frac{5}{3}$

9) (Mackenzie - SP 2003) Se $\log_{\frac{1}{3}}9=a,$ então $\log_{16}a^{2}$ é:

$a)\frac{1}{2}$ $b)\frac{-1}{4}$ $c)-2$ $d)4$ $e)2$

$\log_{\frac{1}{3}}9=a\Rightarrow \left ( \frac{1}{3} \right )^{a}=9\Rightarrow\left (3 ^{-1} \right ) ^{a}=3^{2}\Rightarrow -a=2\Rightarrow a=-2$

Assim, teremos:

$\log_{16}a^{2}=\log_{16}\left ( -2 \right )^{2}=\log_{16}4$

$\log_{16}4=x \Rightarrow 16^{x}=4\Rightarrow \left ( 2^{4} \right )^{x}=2^{2}\Rightarrow 4x=2\Rightarrow x=\frac{2}{4}=\frac{2:2}{4:2}=\frac{1}{2}$

Desta forma, $\log_{16}a^{2}=\frac{1}{2}$ .

A alternativa correta é a a.

2. Condição de existência de um logaritmo

Um logaritmo só existe quando o seu logaritmando é um número positivo e a sua base é um número positivo e diferente de 1. Assim, no logaritmo abaixo teremos:

$\log_{b}a$ , $b> 0$ e $b\neq 1$ e $a> 0$ .

Exemplos:

$\log_{3}-10$ não existe, pois $a=-10$ e a deve positivo para que o logaritmo exista!

$\log_{1}10$ não existe, pois $b=1$ e b deve ser diferente de 1!

3) (PUC - RS) - O conjunto solução da equação $\log_{x}\left ( 10+3x \right )=2$ , em R, é:

$a)\varnothing$ $b)\left \{ -2 \right \}$ $c)\left \{ 5 \right \}$ $d)\left \{-2, 5 \right \}$ $e)\left \{-5, 2 \right \}$

Vamos encontrar os valores de x que satisfaçam as condições de existência deste logaritmo:

$x> 0$ e $x\neq 1$

$10+3x> 0\Rightarrow x> \frac{-10}{3}$

Agora teremos que aplicar a definição de logaritmo:

$\log_{x}\left ( 10+3x \right )=2$

$x^{2}=10+3x\Rightarrow x^{2}-3x-10=0$

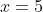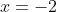Resolvendo a equação do 2º grau, teremos $x=5$ e $x=-2$ , mas somente 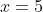$x=5$ satisfaz as condições de existência.

Desta forma, a alternativa correta é a c.

4) ( UFRR - RR 2004) O menor número inteiro pertencente ao domínio da função $f(x)=\log_{x-1}\left ( 5x^{2}-7x-6 \right )$ é um numero:

a) par b) menor que 2 c) múltiplo de 3 d) divisível por 5 e) divisível por 7

Devemos verificar as condições de existência do logaritmo:

$f(x)=\log_{x-1}\left ( 5x^{2}-7x-6 \right )$

( I ) $x-1> 0\Rightarrow x> 1$ e $x-1\neq 1\Rightarrow x\neq 2$

( II )

$5x^{2}-7x-6> 0$

Resolveremos a equação do segundo grau acima e faremos o estudo de sinal da mesma:

$5x^{2}-7x-6=0$

$a=5$ , $b=-7$ e $c=-6$

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=\frac{7\pm \sqrt{\left ( -7 \right )^{2}-4.5.\left ( -6 \right )}}{2.5}=\frac{7\pm \sqrt{169}}{10}=\frac{7\pm 13}{10}$

$x_{1}=\frac{7+13}{10}=2$ $x_{2}=\frac{7-13}{10}=\frac{-6}{10}=\frac{-6:2}{10:2}=\frac{-3}{5}$

Observemos que satisfaremos a condição de existência (II) na parte destacada em azul no gráfico, pois somente nestes intervalos a função terá uma imagem positiva, ou seja, $5x^2-7x-6>0$ .

Ou seja, a condição (II) é válida no seguinte intervalo:

Agora buscaremos a intercessão entre as condições (I) e (II):

Assim, teremos a seguinte solução: $D=]2;+\infty [$

Então, concluímos que o menor número inteiro pertencente ao domínio é o número 3.

Desta forma, a alternativa correta é a c.

5) (UFRR - RR 2004) O domínio da função definida por $f(x)=\sqrt{2x-4}+\log_{10}\left (5x^{2}-7x-6 \right )$

é o intervalo:

$a)]-\infty ,\frac{3}{2}]$ $b)]2,3]$ $c)]2,3[$ $d)]2,+\infty [$ $e)[\frac{3}{2},3 [$

Devemos verificar as condições de existência do logaritmo:

$f(x)=\sqrt{2x-4}+\log_{10}\left ( 5x^{2}-7x-6 \right )$

$(I)2x-4\geq 0\Rightarrow x\geq 2$

☝Obseve que utilizamos o raciocínio acima, pois no campo dos números reais, só existe a raiz de números positivos!

$(II)5x^{2}-7x-6>0$

Resolveremos a equação do segundo grau acima e faremos o estudo de sinal da mesma:

$5x^{2}-7x-6=0$

$a=5$ , $b=-7$ e $c=-6$

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=\frac{7\pm \sqrt{\left ( -7 \right )^{2}-4.5.(-6)}}{2.5}=\frac{7\pm \sqrt{169}}{10}=\frac{7\pm 13}{10}$

$x_{1}=\frac{7+13}{10}=2$ $x_{2}=\frac{7-13}{10}=\frac{-6}{10}=\frac{-3}{5}$

Observemos que satisfaremos a condição de existência (II) na parte destacada em azul no gráfico, pois somente nestes intervalos a função terá uma imagem positiva, ou seja, $5x^2-7x-6>0$ .