Propriedades dos logaritmos e Mudança de Base

1) Propriedades dos logaritmos

1.1.Logaritmo de um produto

O logaritmo de um produto de dois números reais e positivos é igual à soma dos logaritmos destes números:

$\log_{a}\left ( b.c \right )=\log_{a}b+\log_{a}c$

$a> 0$ e $a\neq 1$ , $b> 0$ e $c> 0$

Exemplos:

$1)\log_{10}\left ( 4xy \right )=\log_{10}4+\log_{10}x+\log_{10}y$

$2)\log_{5}15=\log_{5}\left ( 3.5 \right )=\log_{5}3+\log_{5}5=\log_{5}3+1$

$3)\log_{3}78=\log_{3}\left (2.3.13 \right )=\log_{3}2+\log_{3}3+\log_{3}13=\log_{3}2+1+\log_{3}13$

1.2.Logaritmo de um quociente

O logaritmo de um quociente de dois números reais e positivos é igual à diferença dos logaritmos destes números:

$\log_{a}\left ( \frac{b}{c} \right )=\log_{a}b-\log_{a}c$

Exemplos:

$1)\log_{10}5=\log_{10}\left ( \frac{10}{2} \right )=\log_{10}10-\log_{10}2=1-\log_{10}2$

$2)\log_{10}1,2=\log_{10}\left ( \frac{12}{10} \right )=\log_{10}\left ( \frac{12:2}{10:2} \right )=\log_{10}\left ( \frac{6}{5} \right )$

Sendo assim, teremos:

$\log_{10}1,2=\log_{10}6-\log_{10}5=\log_{10}\left ( 2.3 \right )-\log_{10}\left ( \frac{10}{2} \right )$

$\log_{10}1,2=\log_{10}2+\log_{10}3-\left ( \log_{10}10-\log_{10}2 \right )$

$\log_{10}1,2=\log_{10}2+\log_{10}3-\left ( 1-\log_{10}2 \right )=2\log_{10}2+\log_{10}3-1$

3) (Mackenzie - SP 2003) Se $\log_{}x=0,1$ , $\log_{}y=0,2$ e $\log_{}z=0,3$ , o valor de $\log_{}\frac{x^{2}.y^{-1}}{\sqrt{z}}$ é:

$a) 0,15$ $b) -0,15$ $c) 0,25$ $d) -0,25$ $e) 0,6$

$\log_{}\frac{x^{2}.y^{-1}}{\sqrt{z}}=\log_{}x^{2}+\log_{}y^{-1}-\log_{}\sqrt{z}$

$\log_{}\frac{x^{2}.y^{-1}}{\sqrt{z}}=2.\log_{}x+\left ( -1 \right ).\log_{}y-\log_{}z^{\frac{1}{2}}$

$\log_{}\frac{x^{2}.y^{-1}}{\sqrt{z}}=2.\log_{}x+\left ( -1 \right ).\log_{}y-\frac{1}{2}.\log_{}z$

$\log_{}\frac{x^{2}.y^{-1}}{\sqrt{z}}=2.(0,1)-1.(0,2)-\frac{1}{2}.(0,3)=-0,15$

Desta forma, a alternativa correta é a b.

1.3.Logaritmo de uma potência

O logaritmo de uma potência é igual ao produto do expoente pelo logaritmo da base da potência:

$\log_{a}b^{k}=k.\log_{a}b$

$a> 0$ e $a\neq 1$ , $b> 0$ e $k\epsilon R$ .

Caso especial:

$\log_{a}\sqrt[n]{b}=\log_{a}b^{\frac{1}{n}}=\frac{1}{n}.\log_{a}b$

Exemplos:

$1) \log_{2}60=\log_{2}\left ( 2^{2}.3.5 \right )=\log_{2}2^{2}+\log_{2}3+\log_{2}5$

$\log_{2}60=2.\log_{2}2+\log_{2}3+\log_{2}5=2+\log_{2}3+\log_{2}5$

$2)\log_{5}81=\log_{5}3^{4}=4.\log_{5}3$

$3)\log_{10}\sqrt{6}=\log_{10}6^{\frac{1}{2}}=\frac{1}{2}.\log_{10}\left ( 2.3 \right )=\frac{1}{2}.\left (\log_{10}2+\log_{10}3 \right )$

4) (Vunesp - SP) Se $\log_{a}A=2\log_{a}C-\frac{1}{3}\log_{a}D$ , então:

$a)A=\frac{C}{\sqrt[3]{D}}$ $b)A=\frac{3C^{2}}{\sqrt{D}}$ $c)A=\frac{2C}{\sqrt[3]{D}}$ $d)A=\frac{3}{2}.\frac{C}{\sqrt{3}}$ $e)A=C^{2}.\sqrt[3]{D}$

$\log_{a}A=2\log_{a}C-\frac{1}{3}\log_{a}D$

$\log_{a}A=\log_{a}C^{2}-\log_{a}\sqrt[3]{D}=\log_{a}\left ( \frac{C^{2}}{\sqrt[3]{D}} \right )\Rightarrow A=\frac{C^{2}}{\sqrt[3]{D}}$

Desta forma, a alternativa correta é a a.

5) (Unimep - SP) Sendo $\log_{}2=0,3,$ o valor da expressão $\frac{\log_{}16+\log_{}\sqrt{8}}{\log_{}4}$ é:

$a) 1,2$ $b) 2,6$ $c) 1,05$ $d) 2,75$ $e)1$

$\log_{}16=\log_{}2^{4}=4\log_{}2$

$\log_{}\sqrt{8}=\log_{}8^{\frac{1}{2}}=\frac{1}{2}\log_{}8=\frac{1}{2}\log_{}2^{3}=\frac{1}{2}.3.\log_{}2=\frac{3}{2}.\log_{}2$

$\log_{}4=\log_{}2^{2}=2.\log_{}2$

$\frac{\log_{}16+\log_{}\sqrt{8}}{\log_{}4}=\frac{4\log_{}2+\frac{3}{2}\log_{}2}{2\log_{}2}=\frac{4.0,3+\frac{3}{2}.0,3}{2.0,3}=2,75$

Desta forma, a alternativa correta é a d.

6) (UEMS - MS) Se $\log_{}125=k$ , então $\log_{}5$ vale:

$a) 5k$ $b)k ^{5}$ $c)\sqrt[5]{k}$ $d)\frac{k}{3}$ $e)\sqrt{3}k$

$\log_{}125=k\Rightarrow \log_{}5^{3}=k\Rightarrow 3\log_{}5=k\Rightarrow \log_{}5=\frac{k}{3}$

Desta forma, a alternativa correta é a d.

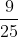7) (UPF - RS) Se $27^{x}=243$ , então o $\log_{}x$ na base $\frac{9}{25}$ é igual a:

$a)0,6$ $b)-1,666$ $c)-2$ $d)-0,5$ $e)-5$

$27^{x}=243\Rightarrow \left ( 3^{3} \right )^{x}=3^{5 }\Rightarrow 3x=5\Rightarrow x=\frac{5}{3}$

Assim, teremos:

$\log_{\frac{9}{25}}x=\log_{\frac{9}{25}}\frac{5}{3}$

$\log_{\frac{9}{25}}\frac{5}{3}=y\Rightarrow \left ( \frac{9}{25} \right )^{y}=\frac{5}{3}\Rightarrow \left ( \left (\frac{3}{5} \right )^{2} \right )^{y}=\left ( \frac{3}{5} \right )^{-1}\Rightarrow 2y=-1$

$\log_{\frac{9}{25}}\frac{5}{3}=y=\frac{-1}{2}=-0,5$

Desta forma, a alternativa correta é a d.

2) Mudança de base

Em algumas situações, devemos trabalhar com algumas bases específicas e, para tal, teremos que realizar a mudança de base do logaritmo da seguinte forma:

$\log_{a}b=\frac{\log_{c}b}{\log_{c}a}$

Exemplos:

$1)\log_{10}8=\frac{\log_{2}8}{\log_{2}10}=\frac{\log_{2}2^{3}}{\log_{2}\left ( 2.5 \right )}=\frac{3.\log_{2}2}{\log_{2}2+\log_{2}5}=\frac{3}{1+\log_{2}5}$

$2)\log_{5}50=\frac{\log_{10}50}{\log_{10}5}=\frac{\log_{10}\left (5 ^{2}.2 \right )}{\log_{10}\left ( \frac{10}{2} \right )}=\frac{\log_{10}5^{2}+\log_{10}2}{\log_{10}10-\log_{10}2}$

$\log_{5}50=\frac{2.\log_{10}5+\log_{10}2}{1-\log_{10}2}=\frac{2.\log_{10}\left ( \frac{10}{2} \right )+\log_{10}2}{1-\log_{10}2}$

$\log_{5}50=\frac{2.\left ( \log_{10}10-\log_{10}2 \right )+\log_{10}2}{1-\log_{10}2}=\frac{2.\left ( 1-\log_{10} 2\right )+\log_{10}2}{1-\log_{10}2}$

$\log_{5}50=\frac{2-2.\log_{10}2+\log_{10}2}{1-\log_{10}2}=\frac{2-\log_{10}2}{1-\log_{10}2}$

3) ( Mackenzie - SP 2004 ) Adotando-se $\log_{}2=0,3,$ então o valor de x, tal que $2^{x+2}=20,$ é:

$a) \frac{7}{3}$ $b) \frac{9}{4}$ $c) \frac{11}{4}$ $d) \frac{5}{3}$ $e) \frac{4}{5}$

$2^{x+2}=20\Rightarrow 2^{x}.2^{2}=20\Rightarrow 2^{x}.4=20\Rightarrow 2^{x}=5\Leftrightarrow \log_{2}5=x$

$\log_{2}\left ( \frac{10}{2} \right )=\log_{2}10-\log_{2}2= \log_{2}10 -1$

Para calcularmos $\log_{2}10$ , mudaremos o logaritmo para a base 10:

$\log_{2}10=\frac{\log_{10}10}{\log_{10}2}=\frac{1}{0,3}=\frac{1}{\frac{3}{10}}=\frac{10}{3}$

Assim, teremos:

$x=\log_{2}5=\log_{2}\left ( \frac{10}{2} \right )=\log_{2}10-1=\frac{10}{3}-1=\frac{10}{3}-\frac{3}{3}=\frac{7}{3}$

Desta forma, a alternativa correta é a a.

4) ( FGV - SP ) Se $y=\left ( \log_{3}2 \right ).\left ( \log_{2}5 \right ).\left ( \log_{5} 9\right )$ , então:

$a) y=1$ $b) y=2$ $c) y=3$ $d) y=\log_{3} 5$ $e) y=\log_{9} 2$

Em primeiro lugar, mudaremos a base de todos os logaritmos:

$\log_{3}2=\frac{\log_{}2}{\log_{}3}$ $\log_{2}5=\frac{\log_{}5}{\log_{}2}$ $\log_{5}9=\frac{\log_{}9}{\log_{}5}=\frac{\log_{}3^{2}}{\log_{}5}=\frac{2.\log_{}3}{\log_{}5}$

$y=\left ( \log_{3}2 \right ).\left ( \log_{2}5 \right ).\left ( \log_{5} 9\right )=\frac{\log_{}2}{\log_{}3}.\frac{\log_{}5}{\log_{}2}.\frac{2\log_{}3}{\log_{}5}=2$

Desta forma, a alternativa correta é a b.

5) (Mackenzie -SP) Se $\frac{1}{\log_{x}3}+\frac{1}{\log_{\sqrt{x}}3}+\frac{1}{\log_{\sqrt[4]{x}}3}+\frac{1}{\log_{\sqrt[8]{x}}3}=\frac{15}{8}$ , então $\log_{3}x$ vale:

$a)\frac{1}{9}$ $b)\frac{1}{3}$ $c)3$ $d)2$ $e)1$

Primeiramente, mudaremos todos os logaritmos para a base 3:

$\log_{x}3=\frac{\log_{3}3}{\log_{3}x}=\frac{1}{\log_{3}x}$ $\log_{\sqrt{x}}3=\frac{\log_{3}3}{\log_{3}\sqrt{x}}=\frac{1}{\log_{3}\sqrt{x}}$

$\log_{\sqrt[4]{x}}3=\frac{\log_{3}3}{\log_{3}\sqrt[4]{x}}=\frac{1}{\log_{3}\sqrt[4]{x}}$ $\log_{\sqrt[8]{x}}3=\frac{\log_{3}3}{\log_{3}\sqrt[8]{x}}=\frac{1}{\log_{3}\sqrt[8]{x}}$

Desta forma,teremos:

$\frac{1}{\log_{x}3}=\frac{1}{\frac{1}{\log_{3}x}}=\log_{3}x$ .

$\frac{1}{\log_{\sqrt{x}}3}=\frac{1}{\frac{1}{\log_{3}\sqrt{x}}}=\log_{3}\sqrt{x}$

$\frac{1}{\log_{\sqrt[4]{x}}3}=\frac{1}{\frac{1}{\log_{3}\sqrt[4]{x}}}=\log_{3}\sqrt[4]{x}$

$\frac{1}{\log_{\sqrt[8]{x}}3}=\frac{1}{\frac{1}{\log_{3}\sqrt[8]{x}}}=\log_{3}\sqrt[8]{x}$

Então, teremos:

$\frac{1}{\log_{x}3}+\frac{1}{\log_{\sqrt{x}}3}+\frac{1}{\log_{\sqrt[4]{x}}3}+\frac{1}{\log_{\sqrt[8]{x}}3}=\frac{15}{8}$

$\log_{3}x+\log_{3}\sqrt{x}+\log_{3}\sqrt[4]{x}+\log_{3}\sqrt[8]{x}=\frac{15}{8}$

$\log_{3}x+\log_{3} x^{\frac{1}{2}}+\log_{3}x^{\frac{1}{4}}+\log_{3}x^{\frac{1}{8}}=\frac{15}{8}$

$\log_{3}x+\frac{1}{2}.\log_{3}x+\frac{1}{4}.\log_{3}x+\frac{1}{8}.\log_{3}x=\frac{15}{8}$

$\log_{3}x\left ( 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8} \right )=\frac{15}{8}$

$\log_{3}x\left ( \frac{8}{8}+\frac{4}{8}+\frac{2}{8}+\frac{1}{8} \right )=\frac{15}{8}$

$\log_{3}x.\left (\frac{15}{8} \right )=\frac{15}{8}$

$\log_{3}x=1$

Desta forma, a alternativa correta é a e.

6) (Mackenzie - SP ) Se $\log_{m}5=a$ e $\log_{m}3=b$ , $0< m\neq 1,$ então $\log_{\frac{1}{m}}\frac{3}{5}$ é igual a:

$a)\frac{b}{a}$ $b)b-a$ $c)3a-5b$ $d)\frac{a}{b}$ $e)a-b$

$\log_{\frac{1}{m}}\frac{3}{5}=\frac{\log_{m}\frac{3}{5}}{\log_{m}\frac{1}{m}}=\frac{\log_{m}3-\log_{m}5}{\log_{m}m^{-1}}=\frac{\log_{m}3-\log_{m}5}{-1.\log_{m}m}=\frac{\log_{m}3-\log_{m}5}{-1}$

$\log_{\frac{1}{m}}\frac{3}{5}=-\log_{m}3+\log_{m}5=-b+a=a-b$

Desta forma,a alternativa correta é a e.

7) (ITA - SP ) Resolver a equação $\log_{5}x+\log_{x}5=\frac{10}{3}$ .

Faremos inicialmente a mudança de base num dos logaritmos:

$\log_{x}5=\frac{\log_{5}5}{\log_{5}x}=\frac{1}{\log_{5}x}$

Agora resolveremos a equação:

$\log_{5}x+\log_{x}5=\frac{10}{3}$

$\log_{5}x+\frac{1}{\log_{5}x}=\frac{10}{3}$

Usaremos uma variável auxiliar $k=\log_{5}x$ :

$\log_{5}x+\frac{1}{\log_{5}x}=\frac{10}{3}$

$k+\frac{1}{k}=\frac{10}{3}\Rightarrow \frac{3k^{2}+3}{3k}=\frac{10k}{3k}\Rightarrow 3k^{2}-10k+3=0$

$k_{1}=3$ $k_{2}=\frac{1}{3}$

$k=\log_{5}x\Rightarrow \log_{5}x=3\Rightarrow x=5^{3}=125$ e $\log_{5}x=\frac{1}{3}\Rightarrow x=5^{\frac{1}{3}}=\sqrt[3]{5}$ .

$V=\left \{ \sqrt[3]{5},125 \right \}$

8) (UFPR-PR) Sabendo que $\log_{12}2=m$ , o valor de $\log_{6}16$ é:

$\log_{12}2=\frac{\log_{2}2}{\log_{2}12}=\frac{1}{\log_{2}\left (2 ^{2}.3 \right )}=\frac{1}{\log_{2}2^{2}+\log_{2}3}=\frac{1}{2\log_{2}2+\log_{2}3}$

$\log_{12}2=\frac{1}{2+\log_{2}3}$

Como temos $\log_{12}2=m$ , então

$m=\frac{1}{\log_{2}3+2}\Rightarrow m.\left (\log_{2} 3+2 \right )=1\Rightarrow m.\log_{2}3+2m=1$

$m.\log_{2}3+2m=1\Rightarrow m.\log_{2}3=1-2m\Rightarrow \log_{2}3=\frac{1-2m}{m}$

Sendo assim, teremos:

$\log_{6}16=\frac{\log_{2}16}{\log_{2}6}=\frac{\log_{2}2^{4}}{\log_{2}\left ( 2.3 \right )}=\frac{4.\log_{2}2}{\log_{2}2+\log_{2}3}=\frac{4}{1+\left ( \frac{1-2m}{m} \right )}$

$\log_{6}16=\frac{4}{1+\left ( \frac{1-2m}{m} \right )}=\frac{4}{\frac{m+1-2m}{m}}=\frac{4}{\frac{-m+1}{m}}=\frac{4m}{1-m}$

Desta forma, a alternativa correta é a a.

Bloglis

Logaritmos - Propriedades e Mudança de Base

Propriedades dos logaritmos e Mudança de Base

1) Propriedades dos logaritmos

1.1.Logaritmo de um produto

1.2.Logaritmo de um quociente

1.3.Logaritmo de uma potência

2) Mudança de base

0 comentários:

Postar um comentário

Labels

Pages

Blog archive

Latest Tweets