Distância entre dois pontos

Dados dois pontos $A(x_{A},y_{A})$ e $B(x_{B},y_{B})$ , podemos calcular a distância entre eles da seguinte forma:

$d=\sqrt{\left ( x_{B}-x_{A} \right )^{2}+\left ( y_{B} -y_{A}\right )^{2}}$

Exemplos:

1) Calcule a distância entre os pontos P (-1,5) e Q (2,0).

$d_{PQ}=\sqrt{\left ( x_{Q} -x_{P}\right )^{2}+\left ( y_{Q}-y_{P} \right )^{2}}$

$d_{PQ}=\sqrt{\left ( 2-(-1) \right )^{2}+\left ( 0-5 \right )^{2}}$

$d_{PQ}=\sqrt{3^{2}+\left ( -5 \right )^{2}}$

$d_{PQ}=\sqrt{34}$

2) ( FASP -SP ) A distância entre os pontos (2,-1) e (-1,3) é igual a:

$a) 0$ $b) \sqrt{5}$ $c) \sqrt{7}$ $d)5$ $e)n.d.a$

$d=\sqrt{\left ( \Delta x \right )^{2}+\left ( \Delta y \right )^{2}}$

$d=\sqrt{\left ( 2-\left ( -1 \right ) \right )^{2}+\left ( -1-3 \right )^{2}}$

$d=\sqrt{3^{2}+\left ( -4 \right )^{2}}$

$d=5$

3) Calcule a distância do ponto A(3;6) à origem do sistema cartesiano.

Origem = O = (0;0)

$d_{AO}=\sqrt{\left (x _{A} -x_{O}\right )^{2}+\left ( y_{A}-y_{O} \right )^{2}}$

$d_{AO}=\sqrt{\left ( 3-0 \right )^{2}+\left ( 6-0 \right )^{2}}$

$d_{AO}=\sqrt{3^{2}+6^{2}}$

$d_{AO}=\sqrt{45}=3\sqrt{5}$

4) Calcule o perímetro do triângulo ABC cujos vértices são A(2,2), B(-4,-6) e C(4,-12).

Observemos o triângulo ABC:

5) ( PUC -SP ) Sendo A(3,1), B(4,-4) e C(-2,2) os vértices de um triângulo, então esse triângulo é:

a) retângulo e não isósceles b) retângulo e isósceles c) equilátero

d) isósceles e não retângulo e) escaleno

$d_{AB}=\sqrt{\left ( 3-4 \right )^{2}+\left ( 1+4 \right )^{2}}=\sqrt{26}$

$d_{AC}=\sqrt{\left ( 3+2 \right )^{2}+\left ( 1-2 \right )^{2}}=\sqrt{26}$

$d_{AC}=\sqrt{\left ( 4+2 \right )^{2}+\left ( -4-2 \right )^{2}}=\sqrt{72}=6\sqrt{2}$

Observemos que temos dois lados com medidas iguais $d_{AB}=d_{AC}$ , logo o triângulo é isósceles. Agora devemos verificar se ele é retângulo:

$\left (d_{BC} \right )^{2}\neq\left (d _{AB} \right ) ^{2}+\left (d _{AC} \right )^{2}$

Logo, este triângulo não é retângulo.

Desta forma, a alternativa correta é a d.

6) Dados A(x,5), B(-2,4) e C(6,6), obtenha x de modo que A seja equidistante de B e C.

$d_{AB}=d_{AC}$

$\sqrt{\left (x _{A}-x_{B} \right )^{2}+\left (y _{A} -y_{B}\right )^{2}}=\sqrt{\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}}$

$\left (\sqrt{\left (x _{A}-x_{B} \right )^{2}+\left (y _{A} -y_{B}\right )^{2}} \right )^{2}=\left (\sqrt{\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}} \right ) ^{2}$

$\left ( x_{A}-x_{B} \right )^{2}+\left ( y_{A} -y_{B}\right )^{2}=\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}$

$\left ( x-\left ( -2 \right ) \right )^{2}+\left ( 5-4 \right )^{2}=\left ( x-6 \right )^{2}+\left ( 5-6 \right )^{2}$

$\left ( x+2 \right )^{2}+ 1^{2}=\left ( x-6 \right )^{2}+\left ( -1 \right )^{2}$

$x^{2}+4x+4+1=x^{2}-12x+36+1$

$4x+4=-12x+36$

$16x=32\Rightarrow x=2$

7) ( FGV - SP 2004 ) No plano cartesiano, o ponto P que pertence à reta de equação y = x e é equidistante dos pontos A(-1,3) e B(5,7) tem abscissa igual a:

a) 3,1 b) 3,3 c) 3,4 d)3,5 e) 3,2

$\sqrt{\left (x _{A}-x_{P} \right )^{2}+\left ( y_{A}-y_{P} \right )^{2}}=\sqrt{\left (x _{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}}$

$\left (\sqrt{\left (x _{A}-x_{P} \right )^{2}+\left ( y_{A}-y_{P} \right )^{2}} \right )^{2}=\left (\sqrt{\left (x _{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}} \right )^{2}$

$\left ( x_{A}-x_{P} \right )^{2}+\left (y _{A} -y_{P}\right )^{2}=\left (x _{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}$

$\left ( -1-x \right )^{2}+\left ( 3-x \right )^{2}=\left ( 5-x \right )^{2}+\left ( 7-x \right )^{2}$

$\left ( x^{2}+2x+1 \right )+\left ( x^{2}-6x+9 \right )=\left ( x^{2}-10x+25 \right )+\left (x ^{2}-14x+49 \right )$

$2x^{2}-4x+10=2x^{2}-24x+74$

$20x=64$

$x=\frac{64}{20}=3,2$

Desta forma, a alternativa correta é a e.

8) ( UFSC - SC ) Dados os pontos A(-1,-1), B(5,-7) e C(x,2), determine x sabendo que o ponto C é equidistante dos pontos A e B.

a) x = 8 b) x = 6 c) x = 15 d) x = 12 e) x = 7

Como C é equidistante de A e B, temos:

$d_{AC}=d_{BC}$

$\sqrt{\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}}=\sqrt{\left ( x_{B}-x_{C} \right )^{2}+\left ( y_{B}-y_{C} \right )^{2}}$

$\left (\sqrt{\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}} \right )^{2}=\left (\sqrt{\left ( x_{B}-x_{C} \right )^{2}+\left ( y_{B}-y_{C} \right )^{2}} \right )^{2}$

$\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}=\left ( x_{B}-x_{C} \right )^{2}+\left ( y_{B} -y_{C}\right )^{2}$

$\left (1-x \right )^{2}+\left (-1-2 \right )^{2}=\left (5-x\right )^{2}+\left ( -7 -2\right )^{2}$

$\left ( x^{2}+2x+1 \right )+9=\left ( x^{2} -10x+25\right )+81$

$2x+10=-10x+106$

$12x=96$

$x=8$

Desta forma, a alternativa correta é a a.

9) ( Cefet - MG 2003 ) Um ponto P que está sobre a curva 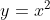$y=x^{2}$ e está equidistante dos pontos A(0,5) e B(3,4) é:

$a) \left ( \sqrt{3},3 \right )$ $b)\left ( 2,4 \right )$ $c)\left ( \sqrt{5},5 \right )$ $d)\left ( \sqrt{6},6 \right )$ $e)\left ( 3,9 \right )$

Como o ponto P pertence à curva 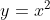$y=x^{2}$ , temos:

$P=\left ( x,y \right )=\left ( x,x^{2} \right )$

P é equidistante de A e B, então temos:

$d_{AP}=d_{BP}$

$\sqrt{\left ( x_{A}-x_{P} \right )^{2}+\left ( y_{A}-y_{P} \right )^{2}}=\sqrt{\left ( x_{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}}$

$\left (\sqrt{\left ( x_{A}-x_{P} \right )^{2}+\left ( y_{A}-y_{P} \right )^{2}} \right )^{2}=\left (\sqrt{\left ( x_{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}} \right )^{2}$

$\left (x _{A} -x_{P}\right )^{2}+\left ( y_{A}-y_{P} \right )^{2}=\left (x _{B}-x_{P} \right )^{2}+\left ( y_{B}-y_{P} \right )^{2}$

$\left (0 -x\right )^{2}+\left (5-x^{2} \right )^{2}=\left (3-x \right )^{2}+\left ( 4-x^{2} \right )^{2}$

$x^{2}+\left ( x^{4}-10x^{2}+25 \right )=\left (x ^{2}-6x+9 \right )+\left ( x^{4}-8x^{2}+16 \right )$

$-10x^{2}+25=-8x^{2}-6x+25$

$-2x^{2}+6x=0\Rightarrow -2x(x-3)=0$

$x=0$ ou $x=3$

Assim, temos:

$P=\left ( x,x^{2} \right )$

$P=\left ( 0,0 \right )$ ou $P=\left ( 3,9 \right )$ .

Desta forma, a alternativa correta é a e.

10) ( Vunesp - SP 2003 ) O triângulo PQR, no plano cartesiano, de vértices P = (0,0), Q = (6,0) e

R = (3,5), é:

a) equilátero b) isósceles, mas não equilátero c) escaleno d) retângulo e) obtusângulo

Para verificarmos qual é a classificação do triângulo PQR quanto aos seus lados, calcularemos as distâncias entre os seus vértices:

$d_{PQ}=\sqrt{\left ( x_{P}-x_{Q} \right )^{2}+\left ( y_{P}-y_{Q} \right )^{2}}$

$d_{PQ}=\sqrt{\left (0-6 \right )^{2}+\left (0-0 \right )^{2}}=\sqrt{36}=6$

$d_{RQ}=\sqrt{\left ( x_{R}-x_{Q} \right )^{2}+\left ( y_{R}-y_{Q} \right )^{2}}$

$d_{RQ}=\sqrt{\left (3-6 \right )^{2}+\left (5-0 \right )^{2}}=\sqrt{34}$

$d_{PR}=\sqrt{\left ( x_{P}-x_{R} \right )^{2}+\left ( y_{P}-y_{R} \right )^{2}}$

$d_{PR}=\sqrt{\left (0-3 \right )^{2}+\left (0-5 \right )^{2}}=\sqrt{34}$

Observemos que o triângulo PQR possui dois lados com medidas iguais e um lado com medida diferente. Trata-se de um triângulo isósceles.

Desta forma, a alternativa correta é a b.

11) ( FGV ) No plano cartesiano, o triângulo de vértices A(1,-2), B(m,4) e C(0,6) é retângulo em A. O valor de m é igual a:

a) 47 b) 48 c) 49 d) 50 e) 51

Observemos o triângulo representado abaixo:

O triângulo ABC é retângulo:

$\left ( d_{BC} \right )^{2}=\left ( d_{AB} \right )^{2}+\left ( d_{AC} \right )^{2}$

Calcularemos primeiramente as medidas dos lados:

$d_{AB}=\sqrt{\left ( x_{A}-x_{B} \right )^{2}+\left ( y_{A}-y_{B} \right )^{2}}$

$d_{AB}=\sqrt{\left (1-m\right )^{2}+\left (-2-4 \right )^{2}}=\sqrt{m^{2}-2m+37}$

$d_{AC}=\sqrt{\left ( x_{A}-x_{C} \right )^{2}+\left ( y_{A}-y_{C} \right )^{2}}$

$d_{AC}=\sqrt{\left (1-0\right )^{2}+\left (-2-6 \right )^{2}}=\sqrt{65}$

$d_{BC}=\sqrt{\left ( x_{B}-x_{C} \right )^{2}+\left ( y_{B}-y_{C} \right )^{2}}$

$d_{BC}=\sqrt{\left (m-0\right )^{2}+\left (4-6 \right )^{2}}=\sqrt{m^{2}+4}$

$\left ( d_{BC} \right )^{2}=\left ( d_{AB} \right )^{2}+\left ( d_{AC} \right )^{2}$

$\left ( \sqrt{m^{2}+4} \right )^{2}=\left ( \sqrt{m^{2}-2m+37} \right )^{2}+\left ( \sqrt{65} \right )^{2}$

$m^{2}+4=m^{2}-2m+37+65$

$2m=98\Rightarrow m=49$

Desta forma,a alternativa correta é a c.

12) ( Vunesp - SP 2003 ) Dados dois pontos, A e B, com coordenadas cartesianas (-2,1) e (1,-2), respectivamente, conforme a figura:

a) calcule a distância entre A e B.

b) sabendo-se que as coordenas cartesianas do baricentro do triângulo ABC são $\left ( x_{G},y_{G} \right )=\left ( \frac{2}{3},1 \right )$ , calcule s coordenadas $\left ( x_{C},y_{C} \right )$ do vértice C do triângulo.

$d_{AB}=\sqrt{\left ( -2-1 \right )^{2}+\left ( 1-\left ( -2 \right ) \right )^{2}}=\sqrt{18}=3\sqrt{2}$

O baricentro de um triângulo é o ponto de encontro das medianas e suas coordenadas são calculadas da seguinte forma:

$x_{G}=\frac{x_{A}+x_{B}+x_{C}}{3}$ $y_{G}=\frac{y_{A}+y_{B}+y_{C}}{3}$

$x_{G}=\frac{x_{A}+x_{B}+x_{C}}{3} \Rightarrow \frac{2}{3}=\frac{-2+1+x_{C}}{3}\Rightarrow x_{C}=3$

$y_{G}=\frac{y_{A}+y_{B}+y_{C}}{3} \Rightarrow 1=\frac{1+\left ( -2 \right )+y_{C}}{3}\Rightarrow y_{C}=4$

Sendo assim, temos: $C =\left ( 3;4 \right )$

Ponto médio de um segmento

O ponto médio de um segmento $M(x_{M},y_{M})$ pode ser encontrado da seguinte forma:

$x_{M}=\frac{x_{A}+x_{B}}{2}$ $y_{M}=\frac{y_{A}+y_{B}}{2}$

Exemplos:

1) Dado o triângulo ABC abaixo, determine o comprimento da mediana AM.

Pelo gráfico acima, primeiramente vamos determinar as coordenadas dos vértices do triângulo:

A(2;2) B(3;4) C(5;-2).

Pelo gráfico, também podemos determinar as coordenadas do ponto M ( ponto médio do segmento BC). Mas vou calcular suas coordenadas através da fórmula apresentada anteriormente:

$x_{M}=\frac{x_{B}+x_{C}}{2}=\frac{3+5}{2}=4$ $y_{M}=\frac{y_{B}+y_{C}}{2}=\frac{4+(-2)}{2}=1$

Assim, temos: M (4;1).

Agora calcularemos o comprimento da mediana ( distância de A a M):

$d_{AM}=\sqrt{\left ( x_{M}-x_{A} \right )^{2}+\left (y _{M} -y_{A}\right )^{2}}$

$d_{AM}=\sqrt{\left ( 4-2 \right )^{2}+\left ( 1-2 \right )^{2}}$

$d_{AM}=\sqrt{2^{2}+\left ( -1 \right )^{2}}=\sqrt{5}$

2) Dados os vértices consecutivos A(3;-2) e B(7;-2) de um paralelogramo e o ponto E (11/2;-1) de intersecção de suas diagonais, determine os outros vértices deste paralelogramo.