Domínio de uma função
Devemos garantir que as operações indicadas na lei de formação da função sejam possíveis de ser realizadas, ou seja, devemos determinar o domínio da função.
Em algumas situações, teremos que restringir elementos do conjunto dos números reais. Vejamos estas situações:
Desta forma, o domínio da função é dado por:
Exemplos:
1) (Cefet - PR) Se  é uma função de D em R, então D é o conjunto:
é uma função de D em R, então D é o conjunto:
O denominador da fração que representa a função não pode ser igual a zero:
Desta forma, a alternativa correta é a b.
2) Determine o domínio de  .
.
Nesta função não há nenhum tipo de restrição, então teremos como domínio o conjunto dos números reais:
Neste caso, temos raízes quadradas e suas múltiplas, as quais só existem para números positivos no conjunto dos números reais:  .
.
Desta forma, o domínio da função é dada por:
Exemplos:
1) ( PUC - SP ) Qual o domínio da função  ?
?
Resolveremos a equação  :
:
2) Determine o domínio das funções reais:
Neste caso, temos  ( observemos que o zero não entra no domínio, pois a raiz está no denominador):
( observemos que o zero não entra no domínio, pois a raiz está no denominador):
Agora, procuraremos a intersecção entre ( I ) e ( II ) para determinarmos o domínio:
3) ( Mackenzie - SP ) A função real  tem domínio de validade igual a :
tem domínio de validade igual a :
Teremos duas restrições e acharemos a intersecção entre elas para determinar o domínio:
Resolveremos a equação  e faremos o estudo do sinal para verificar onde temos
e faremos o estudo do sinal para verificar onde temos  :
:
Pelo gráfico acima, observamos que  :
:
Resolveremos a equação  e faremos o estudo do sinal para verificar onde temos
e faremos o estudo do sinal para verificar onde temos  :
:
Pelo gráfico acima, observamos que  :
:
Agora encontraremos o domínio da função:
Desta forma, a alternativa correta é a d.
4) ( Uespi - PI 2003 ) O domínio da função real f definida por:
Desta forma, a alternativa correta é a c.
5) ( FMTM - MG) O domínio da função real dada por  é o conjunto:
é o conjunto:
Neste caso, temos duas restrições:
Agora, para determinar o domínio da função,procuraremos a intersecção entre ( I ) e ( II ):
Desta forma, a alternativa correta é a b.
6) ( Uespi - PI 2003 ) A função f definida por  tem por conjunto domínio o intervalo real:
tem por conjunto domínio o intervalo real:
Nesta função, teremos a seguinte restrição:
Conforme os exercícios anteriores, resolveremos a equação  e faremos o estudo do sinal:
e faremos o estudo do sinal:
Desta forma, a alternativa correta é a b.
7) ( ESPM -SP ) Qual o domínio de validade da função  real?
real?
Temos duas restrições nesta função:
Agora, encontraremos a intersecção entre (I) e (II) para definirmos o conjunto domínio da função:
8) ( UFRGS - RS 2003) Se x é um número real, então  nunca assume o valor:
nunca assume o valor:
A única restrição que temos neste caso é que o denominador não pode ser igual a zero:
Desta forma, a alternativa correta é a b.
9) ( Unifei - MG 2003 ) A soma S de todos os valores inteiros de x que pertencem ao domínio da função 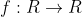 definida por
definida por  é igual a :
é igual a :
A única restrição que temos nesta função é:
A partir do gráfico acima, temos que  no intervalo destacado em azul: ]-4;6[.
no intervalo destacado em azul: ]-4;6[.
Este intervalo representa o domínio da função: 
Valores inteiros de x que pertencem ao domínio: {-3;-2;-1;0;1;2;3;4} e a soma destes valores é igual a 9.
Desta forma, a alternativa correta é a c.
10) ( UFRGS - SP ) O domínio da função real de variável real definida por  é o intervalo:
é o intervalo:
A restrição que temos nesta função é a seguinte:
A partir do gráfico acima, temos que  no intervalo destacado em amarelo: [-3;1].
no intervalo destacado em amarelo: [-3;1].
Este intervalo representa o domínio da função:  .
.
Desta forma, a alternativa correta é a d.
11) ( Fuvest - SP ) Considere a função f dada por  . Determine o seu domínio de validade.
. Determine o seu domínio de validade.
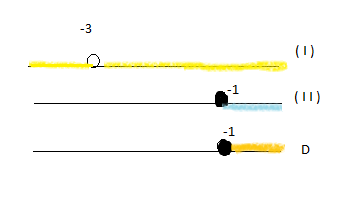
Para efetuarmos os nossos cálculos, chamaremos o numerador de ( I ) e o denominador de ( II ):
Desta forma, a função f é dada por:
Então temos:
( A )  e ( B )
e ( B )  .
.
(A)
(B)
Desta forma, o domínio de vaidade da função f é dado por:

















0 comentários:
Postar um comentário