Funções
1. Notação de funções
Uma função é uma relação binária de A em B, ou seja, é um conjunto de pares ordenados. Dados dois conjuntos A e B, não-vazios, uma função é uma relação binária de A em B de tal maneira que todo elemento pertencente a A tenha um único correspondente em B.
A função costuma ser expressa por uma sentença aberta y = f(x) ( sua lei de formação). A lei de formação de uma função permite que, dado  , se determine
, se determine  , tal que
, tal que  , ou seja:
, ou seja:
Para indicar uma função f, definida em A com imagens em B, podemos usar as seguintes notações:
Exemplos:
2. Conceitos importantes
Par ordenado: par de valores 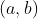 . Quando usamos um par ordenado em funções, normalmente o utilizamos para representar pontos em seu gráfico.
. Quando usamos um par ordenado em funções, normalmente o utilizamos para representar pontos em seu gráfico.
Produto cartesiano: conjunto de todos os possíveis pares ordenados, de forma que o primeiro elemento pertença a um conjunto A e o segundo elemento pertença ao conjunto B:
Exemplo: Dados os conjuntos A={1,3,5} e B={2,4}, o produto cartesiano A x B será dado por:
A x B = { (1,2), (1,4). (3,2), (3,4), (5,2), (5,4)}.
Diagrama de flechas: o produto cartesiano pode ser representado por um diagrama de flechas, no qual as flechas partem do primeiro elemento para o segundo elemento do par ordenado.
Exemplo: Representaremos o produto cartesiano A x B = { (1,2), (1,4). (3,2), (3,4), (5,2), (5,4)} num diagrama de flechas:
Reconhecimento de uma função através de um diagrama de flechas: Uma relação binária representada por um diagrama de flechas para ser uma função deve:
( I ) possuir todos os elementos do conjunto A como ponto de partida de uma flecha;
( II ) a flecha deve ser única.
Exemplos:
1)
É uma função, pois satisfaz as condições apresentadas anteriormente.
2)
É uma função, pois satisfaz as condições apresentadas anteriormente.
3)
Não é uma função, pois não parte nenhuma flecha do elemento c.
4)
Não é uma função, pois partem duas flechas do elemento 3.
Plano cartesiano: normalmente representamos o produto cartesiano no plano cartesiano. No plano cartesiano, temos um sistema de eixos ( eixo x - eixo das abscissas e eixo y - eixo das ordenadas), no qual o primeiro elemento de um par ordenado é colocado no eixo x e o segundo elemento no eixo y. Vejamos o produto cartesiano do exemplo anterior no plano cartesiano:
Domínio de uma função: conjunto de elementos escolhidos para calcularmos as imagens correspondentes através da lei de formação da função. É o conjunto das abscissas ( x ) dos pontos do gráfico de uma função.
Imagem de uma função: Se temos o par ordenado (a,b) pertencente à função, b será a imagem de a, ou seja,  . É o conjunto das ordenadas ( y ) dos pontos do gráfico de uma função.
. É o conjunto das ordenadas ( y ) dos pontos do gráfico de uma função.
Contradomínio de uma função: conjunto no qual encontraremos todas as imagens dos elementos do domínio de uma função, além de outros elementos.
Todos os elementos do domínio devem possuir um elemento correspondente no conjunto do contradomínio, pois caso contrário, a lei de formação não representará uma função.
Exemplos:
1) Seja a função  , qual é a imagem de 0?
, qual é a imagem de 0?
Devemos calcular a imagem de 0, ou seja,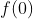 :
:
2) Seja a função de R em R definida abaixo
Calcule:
Observemos que 1 é um número racional  , então teremos
, então teremos 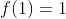 .
.
Observemos que 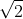 é um número irracional , então teremos
é um número irracional , então teremos  .
.
3) Seja a função  de R em R definida por
de R em R definida por  , calcule o domínio que tem como imagem 79.
, calcule o domínio que tem como imagem 79.
A partir da lei de formação da função : e da informação dada
e da informação dada  , calcularemos o domínio (x):
, calcularemos o domínio (x):
* Neste caso, temos dois valores para o domínio (  e
e 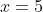 ), pois estamos trabalhando com uma equação do segundo grau, ou seja, uma função quadrática!
), pois estamos trabalhando com uma equação do segundo grau, ou seja, uma função quadrática!
❤Teremos um post específico sobre o tema de funções quadráticas!
4) A função  de R em Ré dada por
de R em Ré dada por  , para todo
, para todo 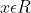 . Se
. Se  , calcule
, calcule 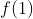 .
.
5) Dado o conjunto  , determine o conjunto B das imagens dos elementos contidos em A, segundo a função
, determine o conjunto B das imagens dos elementos contidos em A, segundo a função  de
de  em
em  , com
, com  .
.

6) Vejamos alguns gráficos de algumas funções e os conjuntos domínio e imagem de cada uma dessas funções:
a)
b) 
7) (UFam - AM 2004) O consumo (C) de uma família e sua renda (x) são tais que C = 1000 + 0,6x. Podemos então afirmar que:
a) Se a renda diminuir em 1000, o consumo diminui em 1600.
b) Se a renda aumenta em 100, o consumo aumenta em 100.
c) Se a renda diminui em 100, o consumo diminui em 100.
d) Se a renda aumenta em 1000, o consumo aumenta em 600.
e) Se a renda dobra, o consumo dobra.
A alternativa correta é a d, pois temos:
O consumo inicial era de 1000 e agora é de 1600, logo o consumo aumenta em 600.
8) ( Mackenzie - SP 2004 ) Se  , então
, então  pertence ao intervalo:
pertence ao intervalo:
a) [0,004;0,006] b) [0,02;0,03] c) [0;0,001] d)[0,002;0,003] e) [0,04;0,05]
Assim, f(10) pertence ao intervalo [0,002;0,003]. A alternativa correta é a d.
9) ( Vunesp - SP 2003 ) Uma função de variável real satisfaz a condição  , qualquer que seja a variável x. Sabendo-se que
, qualquer que seja a variável x. Sabendo-se que  , determine o valor de:
, determine o valor de:
10) ( FAAP - SP) Durante um mês, o número y de unidades produzidas de um determinado bem de consumo é função do número x de funcionários empregados de acordo com a lei  . Sabendo-se que 121 funcionários estão empregados, o acréscimo na produção,com a admissão de 48 novos funcionários, será de:
. Sabendo-se que 121 funcionários estão empregados, o acréscimo na produção,com a admissão de 48 novos funcionários, será de:
a) 550 unidades b) 250 unidades c) 100 unidades d) 650 unidades e) 200 unidades
Para 121 funcionários ( x = 121), teremos a seguinte produção:
Com a admissão de 48 novos funcionários, teremos 169 funcionários ( x = 169 ) e a produção será dada por:
Sendo assim, houve um acréscimo de 100 unidades na produção.
Desta forma, a alternativa correta é a c.
11) ( FEI - SP ) Se  , então
, então 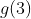 vale:
vale:
a) 0 b) 3 c) 1/2 d) 3/10 e) 2/5
Desta forma, a alternativa correta é a e.
12) ( UFPB - PB 2003 ) Em uma indústria de autopeças, o custo de produção de peças é de R$12,00 fixo mais um custo variável de R$0,70 por cada unidade produzida. Se em um mês foram produzidas x peças, então a lei que representa o custo total dessas x peças é:
a) f(x) = 0,70 - 12x b) f(x) = 12 - 0,70x c) f(x) = 12+0,70x
d) f(x) = 0,70 + 12x e) 12. 0,70x
Desta forma, a alternativa correta é a c.
13) ( UFMS - MS 2004) Para custear seus estudos, um estudante oferece serviços de digitação de textos. O preço a ser pago pela digitação de um texto inclui uma parcela fixa e outra parcela que depende do número de páginas digitadas. Se a parcela fixa for de R$4,00 e cada página digitada custar R$1,60, então a quantidade de páginas digitadas de um texto,cujo serviço de digitação custou R$39,20, será igual a:
a) 29 b) 24 c) 25 d) 20 e) 22
Desta forma, a alternativa correta é a e.
3. Gráfico de uma função
Para construirmos o gráfico de uma função, basta escolhermos alguns pontos do domínio e calcularmos suas respectivas imagens utilizando a lei de formação da função.
Assim, obteremos alguns pares ordenados, os quais colocaremos no plano cartesiano e veremos o comportamento da função.
Exemplos:
Escolheremos alguns pontos do domínio e encontraremos as suas respectivas imagens.
Neste caso, escolhemos x= -1, x=0 e x=1.
Agora, colocaremos cada par ordenado (x,y) no plano cartesiano.
Pontos (pares ordenados:
Escolheremos alguns pontos do domínio e encontraremos as suas respectivas imagens.
Neste caso, escolhemos x= -2, x=0 e x=1.

❤ Em breve, farei outros posts sobre funções!














- Follow Us on Twitter!
- "Join Us on Facebook!
- RSS
Contato