Ângulos

1. Ângulos opostos pelo vértice

Neste caso, temos as retas r e s cruzando-se e formandoos  ângulos a e b opostos pelo vértice.

Observemos uma explicação para o fato de ângulos O.P.V. serem iguais:

Os ângulos a e c são suplementares, ou seja, a+c = 180 º. Os ângulos b e c também o são. Desta forma, temos:

2. Ângulos correspondentes

Neste caso, temos duas retas paralelas cortadas por uma transversal, conforme ilustrado na figura abaixo.

3. Ângulos alternos internos

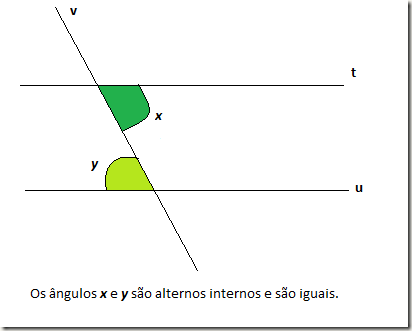
Neste caso, temos duas retas paralelas  cortadas por uma reta transversal.

Exemplos:
1. Calcule a medida desconhecida.
a)

b)

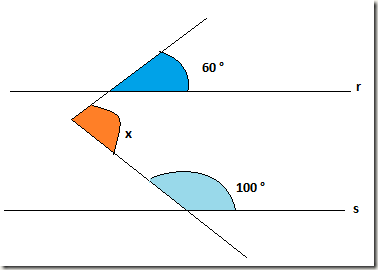
c)

Resolução:
Primeiramente traçamos uma reta t paralela a r e a s. Também encontramos o ângulo suplementar de 100° ( em azul mais escuro).

Desta forma, x = u+v e, como t//r, temos:



d)

Observemos que as retas s e t são paralelas, portanto, podemos concluir que 3x+10° e x+30° são ângulos correspondentes.

Desta forma, tanto o ângulo em azul quanto o ângulo em rosa medem 40°.
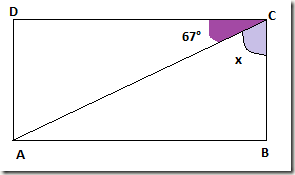
e)

Neste caso, temos um retângulo, logo o ângulo C mede 90°. Desta forma:

Frações–operações

Adição e subtração de frações

Quando os denominadores das frações são iguais, basta somarmos ou subtrairmos os numeradores e mantermos o denominador.
Exemplos:

       

Quando os denominadores das frações são diferentes, devemos reduzí-las a um mesmo denominador. Para tal, devemos encontrar o menor denominador comum entre os denominadores.
Exemplos:
1.

Observe que além de encontrarmos um denominador comum para as frações, temos que dividir o denominador encontrado por cada um dos denominadores e multiplicar pelos respectivos numeradores:

          
Encontrando o denominador comum:

2.

 

3.

    

4.  Que fração subtraída de 1/8 resulta em 1/3?

Verfificação:

Multiplicação de frações

Neste tipo de operação, basta multipliarmos numerador por numerador e denominador por denominador. Vejamos alguns exemplos.
1.

2.

3.

Observe que neste  exemplo fizemos uma simplificação:

4.

5.  Em uma pesquisa, verificou-se que 3/5 dos entrevistados liam a revista
A.  Do restante dos entrevistados, 1/10 liam a revista B. Sabendo-se que foram entrevistadas 125 pessoas, quantas pessoas são leitoras da revista B?

Conforme os dados do problema,  1/1o do restante (125  -  75) dos entrevistados são leitores da revista B :

Assim, concluimos que somente 5 pessoas lêem a revista B.

Divisão de frações

Nesta operação, devemos manter a primeira fração e multiplicá-la pelo inverso da segunda fração. Vejamos alguns exemplos.
1.

2.

3.

4.

Aqui temos uma equação a ser resolvida.